Corso di Analisi Numerica
|
|
|
- Valerio Brunelli
- 8 anni fa
- Visualizzazioni
Transcript
1 Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 8 - METODI ITERATIVI PER I SISTEMI LINEARI Lucio Demeio Dipartimento di Scienze Matematiche
2 1 Norme e distanze 2 3 4
3 Norme e distanze Norme Una norma in R n è una funzione. : R n R tale che x 0 x R n ; x = 0 x = 0; αx = α x ; x + y x + y ; Considereremo due norme notevoli in R n : La norma l 2 (o norma euclidea): se x = (x 1, x 2,..., x n ) T x 2 = n i=1 x2 i ; La norma l (norma infinito): x = max 1 i n x i La norma l 2 rappresenta la (ben nota) distanza euclidea dall origine. In R 2, il luogo dei punti (vettori) per i quali x 2 R è un cerchio di raggio R, mentre il luogo dei punti per i quali x R è un quadrato di lato R.
4 Norme e distanze Esempio con le norme Sia x = ( 1, 2, 0). Allora: x 2 = 5 e x = 2. Verifiche È facile verificare che le norme l 2 ed l soddisfano le proprietà elencate all inizio. Per esempio, x + y = max 1 i n x i + y i max 1 i n ( x i + y i ) max 1 i n x i + max 1 i n y i = x + y x + y 2 2 = X (x i + y i) 2 = X (x 2 i + yi x i y i) i=1,n i=1,n x y x 2 y 2 e quindi x + y 2 x 2 + y 2 Nel penultimo passaggio è stata applicata la disuguaglianza di Cauchy-Schwarz: x T y x y.
5 Norme e distanze Distanza Dati due vettori x,y R 2, si definisce distanza tra x e y la norma del vettore differenza, d(x,y) = x y Ovviamente, ogni norma porta con sé una distanza. Limiti e convergenza Si dice che una successione di vettori {x (k) } k=1 Rn converge ad un vettore x R n rispetto ad una data norma. se, per ogni ε > 0, esiste un intero N(ε) tale che x (k) x < ε per ogni k N(ε). Theorem La successione {x (k) } R n converge ad x R n rispetto alla norma l se e solo se lim k x (k) i = x i per ogni i = 1, 2,.., n.
6 Norme e distanze Dimostrazione Supponiamo che {x (k) } x rispetto a.. Allora, dato ε > 0, esiste N(ε) t.c., per ogni k N(ε), x (k) x = max 1 i n x (k) i x i < ε. Questo implica che x (k) i x i < ε per ogni i = 1, 2,..., n, e quindi la tesi. Viceversa, sia lim k x (k) i = x i per ogni i = 1,2,.., n Allora, dato ε > 0, esistono N i(ε) t.c. x (k) i x i < ε per k > N i(ε). Sia N(ε) = max 1 i n N i(ε). Se k > N(ε) allora max 1 i n x (k) i x i = x (k) x < ε, che implica la convergenza della successione {x (k) } ad x. Norme equivalenti (senza dimostrazione) Tutte le norme in R n sono equivalenti rispetto alle proprietà di convergenza: se una successione {x (k) } x rispetto a., allora converge rispetto a qualunque altra norma.. Per le norme viste qui, vale la relazione.. 2 n..
7 Norme e distanze Convergenza: esempio Sia Abbiamo {x (k) } = e quindi {x (k) } (1, 2, 0, 0) T. ( 1, k, 3 ) T k 2, e k sin k lim k k = 2 3 lim k k 2 = 0 lim k e k sin k = 0
8 Norme e distanze Norme delle matrici Sia M n lo spazio vettoriale delle matrici reali n n. Una norma su M n è una funzione. : M n R tale che A 0 A M n ; A = 0 A = 0; αa = α A ; A + B A + B ; AB A B ; Distanza Si definisce distanza tra due matrici A e B la norma della differenza A B: d(a,b) = A B
9 Norme e distanze Norme delle matrici (teorema) Se. è una norma sui vettori in R n, allora A = max x =1 Ax = max z 0 Az z è una norma su M n, che viene detta norma naturale o indotta. Da qui in poi, salvo eccezioni, useremo sempre questa norma matriciale. L ultima uguaglianza segue dal fatto che, se z ha norma non nulla, allora z/ z ha norma unitaria. Corollario Dal teorema precedente, segue che, per ogni z 0, per ogni A M n e per ogni norma naturale su M n abbiamo che Az A z.
10 Norme e distanze Norme delle matrici Le norme naturali che considereremo sono quelle indotte dalle norme già viste per i vettori: A = max x =1 Ax A 2 = max x 2=1 Ax 2, dette rispettivamente norma l e norma l 2. Theorem (Norma infinito) Sia A = {a ij } una matrice n n. Si ha allora A = max 1 i n n j=1 a ij
11 Norme e distanze Dimostrazione Dimostriamo che valgono contemporaneamente le due disuguaglianze A max 1 i n n j=1 n a ij e A max 1 i n a ij j=1 Per la prima disuguaglianza, se x è un vettore con x = 1, allora n Ax = max 1 i n (Ax) i = max 1 i n a ij x j max 1 i n n da cui segue la prima disuguaglianza. j=1 j=1 j=1 n a ij x j max 1 i n a ij
12 Norme e distanze Per la seconda disuguaglianza, consideriamo dapprima le somme n j=1 a ij e sia p l intero per cui questa somma assume il massimo, cioè n n a pj = max 1 i n a ij. j=1 Sia x il vettore di componenti x j = 1 se a pj 0 e x j = 1 se a pj < 0. Ovviamente è x = 1, ed inoltre a pjx j = a pj per ogni j = 1,2,..., n. Pertanto j=1 nx Ax = max 1 i n (Ax) i = max 1 i n a ij x j j=1 nx nx nx a pjx = a pj j = max 1 i n a ij j=1 j=1 da cui segue la seconda disuguaglianza. j=1
13 Norme e distanze Esempio A = a 1j = 13 j=1,n j=1,n j=1,n a 3j = 11 a 5j = 14 a 2j = 12 j=1,n j=1,n a 4j = 10 quindi A = 14.
14 Norme e distanze Esercizio x 1 = n i=1 x i. (a) Verifica delle proprietà: x 1 0 perchè somma di numeri non negativi; x = 0 x 1 = 0 perchè x i = 0 i, e x 1 = 0 x = 0, perchè se x i 0 per qualche i allora P n i=1 αx 1 = P n i=1 α xi = α x 1; x + y 1 = P n i=1 xi + yi P n i=1 (c) Relazione con la norma l 2 : ( n 2 x 2 1 = x i ) = i=1 xi > 0; n x i 2 + x i x j i j i=1 ( xi + yi ) = x 1 + y 1. n x i 2 = x 2 2 i=1
15 Norme e distanze Esercizio A = ( A s = max i,j=1,n a ij. ) ( ) 1 1 B = AB = 1 1 ( ) Quindi A s = 2 B s = 1 AB s = 3 in contraddizione con la proprietà A B A B.
16 Data una matrice quadrata A di dimensione n, un vettore non nullo x R n si dice autovettore di A se esiste un numero λ, reale o complesso, tale che Ax = λx ed in tal caso λ si chiama autovalore di A e l equazione scritta sopra equazione agli autovalori. Tale equazione può anche essere scritta come (A λi)x = 0 e quindi gli autovettori sono le soluzioni non nulle di tale sistema. Siccome si tratta di un sistema omogeneo, esso ammette soluzioni non nulle se e solo se la matrice A λi è singolare, ovvero ha determinante nullo. Gli autovettori sono quei vettori che vengono moltiplicati per uno scalare sotto l azione della matrice, cioè conservano la direzione.
17 Questa condizione fornisce gli autovalori: a 11 λ a a 1n A λi = a 21 a 22 λ... a 2n p n (λ) = 0 a n1 a n2... a nn λ che è un equazione polinomiale di grado n in λ, detta equazione caratteristica. Per il teorema fondamentale dell algebra, p n (λ) possiede n radici, reali o complesse, ciascuna contata con la propria molteplicità. Se la matrice è reale, allora, se z è una radice, lo è pure z. Ricordiamo anche che, se x è un autovettore, anche αx lo è, per qualunque α (reale o complesso), cioè gli autovettori sono determinati a meno di una costante arbitraria. Esempi Mathematica file Iterativi1.nb
18 Raggio spettrale Sia A una matrice n n e siano λ i, i = 1, 2,..., n gli autovalori. Il massimo, in valore assoluto, degli autovalori è detto raggio spettrale: ρ(a) = max 1 i n λ i Ad esempio, se abbiamo A = λ 1 = 1 + i 2, λ 2 = 1 i 2, λ 3 = 4 con λ 1 = 3, λ 2 = 3, λ 3 = 4 e quindi ρ(a) = 4.
19 Theorem (Raggio spettrale) Sia A una matrice n n. Allora A 2 = [ρ(ãa)]1/2 ρ(a) A per ogni norma naturale.. Dimostrazione Dimostriamo solo la seconda parte. Se x è un autovettore appartenente all autovalore λ, con x = 1, abbiamo Ma A x A e quindi Ax = λx = λ x = λ. ρ(a) = max λ A
20 Se A è simmetrica, allora A 2 = ρ(a).
21 Im (λ) ρ (A) O Re (λ)
22 In molte applicazioni, è importante studiare le potenze delle matrici, ed in particolare cosa succede delle potenze successive quando l esponente va all infinito, cioè lim k A k. Si dá allora la seguente definizione: una matrice si dice che è convergente se lim k (Ak ) ij = 0 1 i, j n Theorem () Le seguenti affermazioni sono equivalenti: A è una matrice convergente; esiste una norma naturale t.c. lim n A n = 0; lim n A n = 0 per tutte le norme naturali; ρ(a) < 1; lim n A n x = 0 per ogni x.
23 Ad esempio, la matrice ( è convergente (provare!!). )
24 Metodi classici I metodi iterativi per la soluzione dei sistemi lineari vengono usati in alternativa ai metodi diretti (eliminazione Gaussiana) quando il numero di equazioni/incognite è elevato e la matrice dei coefficienti è sparsa. In tal caso, i metodi iterativi sono più veloci e richiedono meno memorizzazione dei metodi diretti. Un metodo iterativo per risolvere un sistema lineare Ax = b parte, in generale, da una stima iniziale x (0) e costruisce una successione di vettori {x (k) } che converge alla soluzione. Vedremo tre metodi classici: quello di Jacobi, quello di Gauss-Seidel e quello di Gauss-Seidel con rilassamento.
25 Il metodo di Jacobi Consideriamo il sistema Ax = b e scriviamo esplicitamente le equazioni: a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2... a n1 x 1 + a n2 x a nn x n = b n Risolviamo ora la i esima equazione per l incognita diagonale x i, sotto l ipotesi che a ii 0 per ogni i = 1, 2,..., n:
26 Il metodo di Jacobi x 1 = [b 1 (a 12 x a 1n x n)] /a 11 x 2 = [b 2 (a 21 x a 2n x n)] /a x n = [b n (a n1 x 1 + a n2 x )] /a nn ovvero 0 1 x 1 1 X a 1j x j A /a 11 j x 2 2 X a 2j x j A /a 22 j x n n X a nj x j A /a nn j n
27 Il metodo di Jacobi Supponiamo ora di aver ottenuto il vettore {x (k) } della k esima iterazione. L iterazione successiva viene allora data da x (k+1) 1 = x (k+1) 2 =... x (k+1) n = b 1 j 1 b 2 j 2 b n j n a 1j x (k) j a 2j x (k) j a nj x (k) j /a 11 /a 22 /a nn L ipotesi a ii 0 per ogni i è una condizione necessaria (ma non sufficiente!!) per la convergenza del metodo.
28 Il metodo di Jacobi - Esempio 7 x x 2 + x 3 = 18 2 x 1 9 x x 3 = 12 x 1 4 x x 3 = 6 Risolvendo per le ingognite diagonali otteniamo lo schema iterativo: Mathematica file Jacobi.nb x (k+1) 1 = (18 3 x (k) 2 x (k) 3 )/7 x (k+1) 2 = (2 x (k) x (k) 3 12)/9 x (k+1) 3 = (6 x (k) x (k) 2 )/12
29 Il metodo di Gauss-Seidel Riprendiamo lo schema iterativo di Jacobi: 0 x (k+1) 1 = x (k+1) 2 =... x (k+1) n 1 X j 1 2 X j 2 n X j n a 1j x (k) A /a 11 j 1 a 2j x (k) A /a 22 j 1 a nj x (k) A /a nn j 1 È chiaro che, una volta determinato x (k+1) 1 dalla prima equazione, possiamo utilizzare il nuovo valore nelle equazioni successive, al posto di x (k) 1. Lo stesso dicasi per x (k+1) 2 nelle equazioni dalla terza in poi, e così via per le altre incognite.
30 Il metodo di Gauss-Seidel Lo schema iterativo che si ottiene in tal guisa è detto metodo di Gauss-Seidel: x (k+1) 1 = x (k+1) 2 = x (k+1) 3 =... x (k+1) n = b 1 j 1 a 1j x (k) j /a 11 b 2 a 21 x (k+1) 1 j 3 a 2j x (k) j /a 22 b 3 a 31 x (k+1) 1 a 32 x (k+1) 2 j 4 b n j<n a nj x (k+1) j /a nn a 3j x (k) j /a 33
31 ovvero x (k+1) i = i 1 b i j=1 a ij x (k+1) j n j=i+1 a ij x (k) j /a ii
32 Versioni matriciali: Jacobi Il metodo di Jacobi è equivalente a scrivere la matrice dei coefficienti, A, come somma della sua parte diagonale e di quella non diagonale, A = D + R, dove D = a a a nn R = 0 a 12 a a 1n a 21 0 a a 2n a n1 a n2 a n Il sistema Ax = b si può scrivere allora: (D + R)x = b, ovvero Dx = b Rx. Quindi x = D 1 (b Rx) e l algoritmo iterativo di Jacobi si può scrivere come x (k+1) = D 1 (b Rx (k) ) = Tx (k) + c. dove T D 1 R e c = D 1 b.
33 Versioni matriciali: Gauss-Seidel Per il metodo di Gauss-Seidel scriviamo ancora A = D + R, ma poniamo inoltre R = L U, dove a L = a 31 a a n1 a n2 a n a 12 a a 1n 0 0 a a 2n U = a n 1,n
34 Il sistema Ax = b si può scrivere allora: (D L U)x = b, ovvero (D L)x = Ux + b. Quindi x = (D L) 1 (Ux + b) e l algoritmo iterativo di Gauss-Seidel si può scrivere come x (k+1) = (D L) 1 (Ux (k) + b) = Tx (k) + c. dove T (D L) 1 U e c = (D L) 1 b. Forme matriciali Le forme matriciali per il metodo di Jacobi e di Gauss-Seidel torneranno utili per l analisi di convergenza dei metodi.
35 Convergenza dei metodi iterativi Abbiamo visto che i metodi di Jacobi e di Gauss-Seidel in forma matriciale si scrivono x (k+1) = Tx (k) + c, dove T D 1 R per Jacobi e T (D L) 1 U per Gauss-Seidel. Il teorema principale sulla convergenza dice che Theorem Per ogni vettore x (0) R n, la successione {x (k) } definita da x (k+1) = Tx (k) + c, converge all unica soluzione del problema x = Tx + c se e solo se ρ(t) < 1. Per la dimostrazione del teorema, abbiamo bisogno di un lemma preparatorio.
36 Lemma Sia T una matrice n n e sia ρ(t) il suo raggio spettrale. Se ρ(t) < 1 allora la matrice I T è invertibile e (I T) 1 = I + T + T = n=0 T n Dimostrazione Cominciamo con l osservare che, se Tx = λx (cioè se λ è un autovalore di T) allora 1 λ è un autovalore dt I T, infatti (I T)x = (1 λ)x. Ma, per ipotesi, ρ(t) < 1 e quindi λ < 1 per ogni autovalore. Di conseguenza, la matrice I T non ha autovalori nulli ed è invertibile. Sia ora S m = I + T + T T m = P m n=0 Tn. Allora (I T)S m = (I + T + T T m ) (T + T T m+1 ) = I T m+1.
37 Ora, dall ipotesi ρ(t) < 1 segue che T è convergente, e quindi lim (I T)Sm = lim (I m m Tm+1 ) = I da cui (I T) 1 = lim m Sm = X T n n=0 Dimostrazione del teorema Dimostriamo prima che se ρ(t) < 1 la successione converge. Consideriamo la successione x (k) = Tx (k 1) + c = T(Tx (k 2) + c) + c = T 2 x (k 2) + (T + I)c... = T k x (0) + (T k 1 + T k I)c
38 Riassumendo, x (k) = T k x (0) + (T k 1 + T k I)c Ma ρ(t) < 1, quindi T è convergente e quindi lim k Tk x (0) = 0 e quindi, per il lemma precedente, ( ) lim k x(k) = T n c = (I T) 1 c n=0 La successione {x (k) } converge pertanto al vettore x = (I T) 1 c, ed abbiamo x = Tx + c.
39 Supponiamo ora che la successione {x (k) } converga alla soluzione (unica) di x = T x + c e dimostriamo che deve essere ρ(t) < 1. Dimostreremo in realtà l affermazione equivalente che T è convergente. Sia allora z R n arbitrario e sia x la soluzione (unica) di x = Tx + c. Poniamo x (0) = x z e costruiamo la successione x (k) = Tx (k 1) + c; per ipotesi, {x (k) } converge ad x e E pertanto x x (k) = (Tx + c) (Tx (k 1) + c) = T(x x (k 1) ) = T 2 (x x (k 2) ) =... = T k (x x (0) ) = T k z lim k Tk z = lim (x k x(k) ) = 0 che, per l arbitrarietà di z, implica la convergenza di T.
40 Alcuni fatti importanti Elenchiamo di seguito alcuni teoremi sulla convergenza dei metodi iterativi senza dimostrarli; comunque essi seguono dai teoremi visti in precedenza. Sia T < 1 in qualunque norma naturale e sia c R n un vettore dato. Allora la successione {x (k) } data da x (k+1) = Tx (k) + c converge, per ogni x (0) R n ad un vettore x R n e valgono le seguenti limitazioni sull errore: 1 x x (k) T k x (0) x ; 2 x x (k) T k 1 T x(1) x (0) ; Se A è a dominanza diagonale stretta, allora i metodi di Jacobi e di Gauss-Seidel convergono per qualunque scelta della stima iniziale x (0) ; il raggio spettrale dà una misura della rapidità della convergenza del metodo iterativo, x (k) x ρ(t) k x (0) x.
41 Alcuni fatti importanti: teorema di Stein-Rosenberg Indichiamo con T J e T G le matrici T rispettivamente del metodo di Jacobi e di Gauss-Seidel e sia A la matrice dei coefficienti del sistema. Allora, se a ii > 0 per ogni i e a ij 0 per ogni i j, una e solo una delle seguenti affermazioni è vera: 0 ρ(t G ) < ρ(t J ) < 1; 1 < ρ(t J ) < ρ(t G ); ρ(t J ) = ρ(t G ) = 0 ρ(t J ) = ρ(t G ) = 1. Vediamo che, sotto le ipotesi particolari enunciate nel teorema, quando uno dei due metodi converge allora convergono entrambi, Gauss-Seidel facendolo con maggior rapidità (vedi prima affermazione) e che quando un metodo diverge allora divergono entrambi (seconda affermazione).
42 Lucio Demeio condipartimento D, L eddiu Scienze definite Matematiche in precedenza. Il Successive Over Relaxation Method, SOR Dalle considerazioni precedenti, è chiaro che un metodo iterativo converge tanto più rapidamente quanto più piccolo è il raggio spettrale della matrice che lo caratterizza. È pertanto vantaggioso scegliere un metodo iterativo che abbia raggio spettrale il più piccolo possibile. Questo sogno si può realizzare con il metodo del sovrarilassamento (Successive Over Relaxation Method, SOR). Riprendiamo la formula iterativa esplicita (non matriciale) del metodo di Gauss-seidel e riportiamola subito sotto in forma matriciale: x (k+1) i = i 1 b i j=1 a ij x (k+1) j n j=i+1 x (k+1) = D 1 (b + Lx (k+1) + Ux (k) ) a ij x (k) j /a ii
43 Il Successive Over Relaxation Method, SOR Il metodo SOR consiste in una variante del metodo di Gauss-Seidel, in cui il valore x (k+1) viene ottenuto mediante una media pesata tra il valore fornito dall iterazione di Gauss-Seidel (che riportiamo qui sotto per completezza) ed il valore x (k) dell iterazione precedente: x (k+1) = D 1 (b + Lx (k+1) + Ux (k) ) x (k+1) = ω D 1 (b + Lx (k+1) + Ux (k) ) + (1 ω)x (k) dove ω > 0 è un parametro reale, per ora arbitario. Moltiplicando l ultima equazione da sinistra per D, Dx (k+1) = ω (b + Lx (k+1) + Ux (k) ) + (1 ω)dx (k)
44 Riprendiamo: Dx (k+1) = ω (b + Lx (k+1) + Ux (k) ) + (1 ω)dx (k) da cui (D ωl)x (k+1) = (ω U + (1 ω)d)x (k) + ω b x (k+1) = (D ωl) 1 (ω U + (1 ω)d)x (k) +ω (D ωl) 1 b Lo schema iterativo SOR può dunque essere scritto nella usuale forma matriciale x (k+1) = Tx (k) + c, dove T = T ω (D ωl) 1 (ω U + (1 ω)d) e c = c ω ω (D ωl) 1 b
45 Le proprietà di convergenza del metodo dipendono dunque dalla matrice T ω. Nella pratica, però, la versione matriciale è usata solo per l analisi di convergenza; per la stesura degli algoritmi si preferisce la forma esplicita scalare x (k+1) i per i = 1, 2,..., n. = ω i 1 b i a ii j=1 a ij x (k+1) j n j=i+1 a ij x (k) j + (1 ω)x (k) i Convergenza di SOR Al problema di determinare il valore ottimale di ω per un dato sistema Ax = b non si può dare una risposta a priori, e molto si deve lasciare all esperienza. Esistono comunque dei risultati parziali, che valgono in alcune circostanze. Ne citiamo tre dimostrando solo il primo.
46 Theorem (Teorema di Kahan) Sia Ax = b il sistema lineare da risolvere. Se a ii 0 per ogni i, allora ρ(t ω ) ω 1. Pertanto, il metodo iterativo SOR converge solo se 0 < ω < 2. Dimostrazione Ricordiamo che T ω = (D ωl) 1 (ω U + (1 ω)d). Siccome D ωl è una matrice triangolare inferiore i cui elementi diagonali sono gli elementi diagonali di D, abbiamo che Det((D ωl)) = Det(D) e Det((D ωl) 1 ) = Det(D 1 ) e, con ragionamento analogo, Det(ω U + (1 ω)d) = Det((1 ω)d) = (1 ω) n Det(D). Ne segue che Det(T ω) = (1 ω) n e quindi Q n j=1 λj = 1 ω n, con λ j, j = 1,2,..., n gli autovalori di T ω. Quindi, se 1 ω > 1 esiste almeno un autovalore λ con λ > 1 e quindi ρ(t ω) > 1. Allora, non può essere che il massimo, in valore assoluto, degli autovalori sia minore di 1 ω > 1 (altrimenti il prodotto di n numeri tutti minori di 1 ω > 1 non potrebbe dare 1 ω > 1 come risultato) e ne segue la tesi.
47 Theorem (Teorema di Ostrowski-Reich) Sia Ax = b il sistema lineare da risolvere e sia A definita positiva. Allora SOR converge per qualunque scelta iniziale x (0) se e solo se 0 < ω < 2. Theorem Sia Ax = b il sistema lineare da risolvere e sia A definita positiva e tridiagonale. Allora ρ(t G ) = [ρ(t J )] 2 < 1 e la scelta ottimale per il parametro ω di SOR è data da ω = [ρ(t J )] 2.
48 Esercizi Esercizio : Se A è a dominanza diagonale stretta, allora T J < 1. Esercizio : Un oggetto si trova in uno qualunque dei punti equispaziati {x 0, x 1,..., x n}. Quando si trova in x i, può saltare in x i+1 o in x i 1 con la stessa probabilità. Ora, indichiamo con P i la probabilità che l oggetto, partendo dalla posizione x i, raggiunga l estremo x 0 prima di x n. Ovviamente, P 0 = 1 e P n = 0. Siccome l oggetto può giungere in x i solo da x i+1 o da x i 1 e con la stessa probabilità, ne segue che P i = Pi 1 + Pi+1 2 Dimostrare che le probabilità p = (P 1, P 2,..., P n 1) obbediscono ad un sistema lineare Ap = b, e determinare A e b. Risolvere il sistema per n = 10, n = 50 ed n = 100. Cambiare quindi le probabilità di salto in α ed 1 α.
49 CONDIZIONAMENTO
Corso di Calcolo Numerico
 Corso di Calcolo Numerico Dottssa MC De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Corso di Calcolo Numerico - Dottssa MC De Bonis
Corso di Calcolo Numerico Dottssa MC De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Corso di Calcolo Numerico - Dottssa MC De Bonis
Autovalori e Autovettori
 Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2008-2009 Autovalori e Autovettori Definizione Siano A C nxn, λ C, e x C n, x 0, tali che Ax = λx. (1) Allora
Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2008-2009 Autovalori e Autovettori Definizione Siano A C nxn, λ C, e x C n, x 0, tali che Ax = λx. (1) Allora
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Corso di Calcolo Numerico
 Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 8 - METODI ITERATIVI PER I SISTEMI LINEARI Norme Una norma in R n è una funzione. : R n R tale che x 0 x R n ; x = 0 x = 0; αx = α x ; x
Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 8 - METODI ITERATIVI PER I SISTEMI LINEARI Norme Una norma in R n è una funzione. : R n R tale che x 0 x R n ; x = 0 x = 0; αx = α x ; x
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Metodi iterativi per sistemi lineari
 Metodi iterativi per sistemi lineari Dario A. Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi ai metodi iterativi per risolvere sistemi di equazioni
Metodi iterativi per sistemi lineari Dario A. Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi ai metodi iterativi per risolvere sistemi di equazioni
Corso di Matematica per la Chimica
 Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
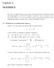 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Documentazione esterna al software matematico sviluppato con MatLab
 Documentazione esterna al software matematico sviluppato con MatLab Algoritmi Metodo di Gauss-Seidel con sovrarilassamento Metodo delle Secanti Metodo di Newton Studente Amelio Francesco 556/00699 Anno
Documentazione esterna al software matematico sviluppato con MatLab Algoritmi Metodo di Gauss-Seidel con sovrarilassamento Metodo delle Secanti Metodo di Newton Studente Amelio Francesco 556/00699 Anno
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
x 1 + x 2 3x 4 = 0 x1 + x 2 + x 3 = 0 x 1 + x 2 3x 4 = 0.
 Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura
 Cognome Nome Matricola ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura (Primo appello/ii prova parziale 15/6/15 - Chiarellotto-Urbinati) Per la II prova: solo esercizi
Cognome Nome Matricola ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura (Primo appello/ii prova parziale 15/6/15 - Chiarellotto-Urbinati) Per la II prova: solo esercizi
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Condizionamento del problema
 Condizionamento del problema x 1 + 2x 2 = 3.499x 1 + 1.001x 2 = 1.5 La soluzione esatta è x = (1, 1) T. Perturbando la matrice dei coefficienti o il termine noto: x 1 + 2x 2 = 3.5x 1 + 1.002x 2 = 1.5 x
Condizionamento del problema x 1 + 2x 2 = 3.499x 1 + 1.001x 2 = 1.5 La soluzione esatta è x = (1, 1) T. Perturbando la matrice dei coefficienti o il termine noto: x 1 + 2x 2 = 3.5x 1 + 1.002x 2 = 1.5 x
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Approssimazione polinomiale di funzioni e dati
 Approssimazione polinomiale di funzioni e dati Approssimare una funzione f significa trovare una funzione f di forma più semplice che possa essere usata al posto di f. Questa strategia è utilizzata nell
Approssimazione polinomiale di funzioni e dati Approssimare una funzione f significa trovare una funzione f di forma più semplice che possa essere usata al posto di f. Questa strategia è utilizzata nell
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
ANALISI DEL CONDIZIONAMENTO DI UN SISTEMA LINEARE
 ANALISI DEL CONDIZIONAMENTO DI UN SISTEMA LINEARE Algebra lineare numerica 121 Ax = b A, b affetti dall errore di round-off si risolve sempre un sistema perturbato: con (A + A)(x + x) = b + b A = ( a i,j
ANALISI DEL CONDIZIONAMENTO DI UN SISTEMA LINEARE Algebra lineare numerica 121 Ax = b A, b affetti dall errore di round-off si risolve sempre un sistema perturbato: con (A + A)(x + x) = b + b A = ( a i,j
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Esempio. Approssimazione con il criterio dei minimi quadrati. Esempio. Esempio. Risultati sperimentali. Interpolazione con spline cubica.
 Esempio Risultati sperimentali Approssimazione con il criterio dei minimi quadrati Esempio Interpolazione con spline cubica. Esempio 1 Come procedere? La natura del fenomeno suggerisce che una buona approssimazione
Esempio Risultati sperimentali Approssimazione con il criterio dei minimi quadrati Esempio Interpolazione con spline cubica. Esempio 1 Come procedere? La natura del fenomeno suggerisce che una buona approssimazione
Federico Lastaria. Analisi e Geometria 2. Matrici simmetriche. Il teorema spettrale. 1/24
 Contenuto Endomorfismi auto-aggiunti. Matrici simmetriche. Il teorema spettrale Gli autovalori di una matrice simmetrica sono tutti reali. (Dimostrazione fatta usando i numeri complessi). Dimostrazione
Contenuto Endomorfismi auto-aggiunti. Matrici simmetriche. Il teorema spettrale Gli autovalori di una matrice simmetrica sono tutti reali. (Dimostrazione fatta usando i numeri complessi). Dimostrazione
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Diagonalizzazione di matrici e applicazioni lineari
 CAPITOLO 9 Diagonalizzazione di matrici e applicazioni lineari Esercizio 9.1. Verificare che v = (1, 0, 0, 1) è autovettore dell applicazione lineare T così definita T(x 1,x 2,x 3,x 4 ) = (2x 1 2x 3, x
CAPITOLO 9 Diagonalizzazione di matrici e applicazioni lineari Esercizio 9.1. Verificare che v = (1, 0, 0, 1) è autovettore dell applicazione lineare T così definita T(x 1,x 2,x 3,x 4 ) = (2x 1 2x 3, x
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
Rette e curve, piani e superfici
 Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
METODI ITERATIVI PER SISTEMI LINEARI
 METODI ITERATIVI PER SISTEMI LINEARI LUCIA GASTALDI 1. Metodi iterativi classici Sia A R n n una matrice non singolare e sia b R n. Consideriamo il sistema (1) Ax = b. Un metodo iterativo per la soluzione
METODI ITERATIVI PER SISTEMI LINEARI LUCIA GASTALDI 1. Metodi iterativi classici Sia A R n n una matrice non singolare e sia b R n. Consideriamo il sistema (1) Ax = b. Un metodo iterativo per la soluzione
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
La Programmazione Lineare
 4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
ESERCIZI APPLICAZIONI LINEARI
 ESERCIZI APPLICAZIONI LINEARI PAOLO FACCIN 1. Esercizi sulle applicazioni lineari 1.1. Definizioni sulle applicazioni lineari. Siano V, e W spazi vettoriali, con rispettive basi B V := (v 1 v n) e B W
ESERCIZI APPLICAZIONI LINEARI PAOLO FACCIN 1. Esercizi sulle applicazioni lineari 1.1. Definizioni sulle applicazioni lineari. Siano V, e W spazi vettoriali, con rispettive basi B V := (v 1 v n) e B W
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Massimi e minimi vincolati
 Massimi e minimi vincolati In problemi di massimo e minimo vincolato viene richiesto di ricercare massimi e minimi di una funzione non definita su tutto R n, ma su un suo sottoinsieme proprio. Esempio:
Massimi e minimi vincolati In problemi di massimo e minimo vincolato viene richiesto di ricercare massimi e minimi di una funzione non definita su tutto R n, ma su un suo sottoinsieme proprio. Esempio:
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Sui concetti di definizione, teorema e dimostrazione in didattica della matematica
 Liceo Scientifico Statale P. Paleocapa, Rovigo XX Settimana della Cultura Scientifica e Tecnologica 19 marzo 2010 Sui concetti di definizione, teorema e dimostrazione in didattica della matematica Prof.
Liceo Scientifico Statale P. Paleocapa, Rovigo XX Settimana della Cultura Scientifica e Tecnologica 19 marzo 2010 Sui concetti di definizione, teorema e dimostrazione in didattica della matematica Prof.
SISTEMI LINEARI QUADRATI: METODI ITERATIVI
 SISTEMI LINEARI QUADRATI: METODI ITERATIVI CALCOLO NUMERICO e PROGRAMMAZIONE SISTEMI LINEARI QUADRATI:METODI ITERATIVI p./54 RICHIAMI di ALGEBRA LINEARE DEFINIZIONI A R n n simmetrica se A = A T ; A C
SISTEMI LINEARI QUADRATI: METODI ITERATIVI CALCOLO NUMERICO e PROGRAMMAZIONE SISTEMI LINEARI QUADRATI:METODI ITERATIVI p./54 RICHIAMI di ALGEBRA LINEARE DEFINIZIONI A R n n simmetrica se A = A T ; A C
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
DOMINI A FATTORIZZAZIONE UNICA
 DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
L espressione torna invece sempre vera (quindi la soluzione originale) se cambiamo contemporaneamente il verso: 1 < 0.
 EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
Matematica generale CTF
 Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
LEZIONE 17. B : kn k m.
 LEZIONE 17 17.1. Isomorfismi tra spazi vettoriali finitamente generati. Applichiamo quanto visto nella lezione precedente ad isomorfismi fra spazi vettoriali di dimensione finita. Proposizione 17.1.1.
LEZIONE 17 17.1. Isomorfismi tra spazi vettoriali finitamente generati. Applichiamo quanto visto nella lezione precedente ad isomorfismi fra spazi vettoriali di dimensione finita. Proposizione 17.1.1.
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
MATEMATICA. { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un numero x ed un numero y che risolvano entrambe le equazioni.
 MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Algebra Lineare e Geometria
 Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Soluzioni del giornalino n. 16
 Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
Soluzioni del giornalino n. 16 Gruppo Tutor Soluzione del Problema 1 Soluzioni corrette ci sono pervenute da : Gianmarco Chinello, Andrea Conti, Simone Costa, Marco Di Liberto, Simone Di Marino, Valerio
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
Equazioni alle differenze finite (cenni).
 AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
1. Sia dato un poliedro. Dire quali delle seguenti affermazioni sono corrette.
 . Sia dato un poliedro. (a) Un vettore x R n è un vertice di P se soddisfa alla seguenti condizioni: x P e comunque presi due punti distinti x, x 2 P tali che x x e x x 2 si ha x = ( β)x + βx 2 con β [0,
. Sia dato un poliedro. (a) Un vettore x R n è un vertice di P se soddisfa alla seguenti condizioni: x P e comunque presi due punti distinti x, x 2 P tali che x x e x x 2 si ha x = ( β)x + βx 2 con β [0,
LE FIBRE DI UNA APPLICAZIONE LINEARE
 LE FIBRE DI UNA APPLICAZIONE LINEARE Sia f:a B una funzione tra due insiemi. Se y appartiene all immagine di f si chiama fibra di f sopra y l insieme f -1 y) ossia l insieme di tutte le controimmagini
LE FIBRE DI UNA APPLICAZIONE LINEARE Sia f:a B una funzione tra due insiemi. Se y appartiene all immagine di f si chiama fibra di f sopra y l insieme f -1 y) ossia l insieme di tutte le controimmagini
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
Ottimizzazione Multi Obiettivo
 Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
