MOMENTI DI INERZIA. m i. i=1
|
|
|
- Graziana Grande
- 8 anni fa
- Visualizzazioni
Transcript
1 MOMENTI DI INEZIA Massa Ad ogni punto materiale si associa uno scalare positivo m che rappresenta la quantità di materia di cui è costituito il punto. m, la massa, è costante nel tempo. Dato un sistema discreto di punti P i, a ciascuno di essi sarà associata la sua massa m i. La massa è additiva, ovvero la massa del sistema è data da P m := N m i. (1) Se il corpo è continuo, si può definire in ogni punto P del corpo una funzione non negativa ρ (P ), la densità, che rappresenta la massa per unità di volume (o di superficie, o di lunghezza) del corpo, la cui massa totale m := ρ (P ) d. (2) entro di Massa Definizione 1 Dato un sistema discreto di N punti materiali di massa m i,oppure un corpo continuo di densità ρ (P ), fissata una origine O, sidicecentrodimassa il punto G individuato dal vettore posizione nel caso discreto, oppure nel caso continuo. m i P i O (3) m i ρ (P ) d ρ (P ) d P O Osservazione 1 La formula del centro di massa è simile alla formula del baricentro. icordiamo che p = m g per corpi con estensione sufficientemente piccola rispetto alle dimensioni della terra. g si può supporre costante. In questo caso i pesi sono un sistema di forze parallele esiste dunque il centro di questo sistema di forze, detto baricentro, che coincide con il centro di massa. Infatti per un sistema discreto p i P i O = p i mentre per un sistema continuo m i /g P i O m i /g κ (P ) d κ (P ) d = P O m i P i O 5 (4), (5) m i, (6)
2 6 dove con κ (P ) indichiamo il peso specifico. Ma κ (P )=ρ (P ) g, quindi ρ (P ) /gd ρ (P ) /gd P O ρ (P ) d = ρ (P ) d P O. (7) Momento d Inerzia Definizione 2 Si definisce momento d inerzia rispetto ad un asse a, la seguente quantità scalare I a := mr 2. (8) Si noti che I a = P a. (9) In generale I a. Definizione 3 Si definisce momento d inerzia per un sistema discreto di N punti rispetto ad un asse a, la seguente quantità scalare P I a := N m i ri 2. (1) In questo caso I a = tutti i punti P i sono sull asse a.
3 Definizione 4 Si definisce momento d inerzia per un sistema continuo rispetto ad un asse a, la seguente quantità scalare 7 I a := r 2 (P ) dm = r 2 (P ) ρ (P ) d. (11) M Esempio 1 Asta omogenea di lunghezza l emassam formante un angolo θ con l asse a. Sia ρ = m/l la densità dell asta. Detto x p un punto generico dell asta, la lunghezza del segmento OP vale r = x p sin θ. AlvariaredelpuntoP sull asta, il momento d inerzia si può scrivere come I a = l Z2 m l r2 dx = l Z2 m l (x sin θ)2 dx = m l sin2 θ l Z2 x 2 dx l 2 l 2 l 2 = m x 3 l sin2 θ 3 l 2 l 2 = m µ l 3 3l sin2 θ = m l sin2 θ. (12) Se l angolo θ = π/2 = I a = m l2 12. (13)
4 8 Esempio 2 Disco omogeneo di raggio emassam Il punto P è individuato dalle coordinate (r, θ) con r e π θ π. alcoliamo l area infinitesima da AB = rdθ A B = drdθ AA = dr da = rdrdθ La distanza del punto generico P dall asse è data da PP = r sin θ e la densità è ρ = M/π 2. Il momento d inerzia rispetto all asse a è Z I a = Z M π π 2 r2 sin 2 θrdθdr = π Z M π 2 r2 sin 2 θrdθdr (stiamo variando r tra e e θ varia tra π e π) Z M π π 2 π sin 2 θ Z r 2 rdr dθ = M π 2 Z π π 4 4 sin2 θdθ = M2 π4 Z π π sin 2 θdθ M 2 Z π π4 2 sin 2 θdθ = M2 π2 Z π 1 cos 2θ dθ 2 = M2 π2 ½ 1 2 [θ]π 1 2 sin 2θ 2 π ¾ = M2 π2 π 2 = M2 4 (14)
5 9 Teorema 1 Sia assegnato il piano π esiaz π, allora I z = I x + I y (15) con x, y qualunque coppia di assi ortogonali appartenenti al piano π passante per l origine O. Dimostrazione. Per definizione I z = Σ x 2 + y 2 ρdσ ρx 2 dσ + ρy 2 dσ = I x + I y. (16) Σ Σ Teorema 2 (di Huygens) (alcolo dei momenti d inerzia rispetto ad assi paralleli) Sia I G il valore del momento d inerzia calcolato rispetto all asse passante per il baricentro G. Indichiamo con d la distanza tra l asse baricentrale e un asse parallelo ad esso. Allora, indicato con I a il momento d inerzia calcolato rispetto all asse a, vale la relazione I a = I G + md 2. (17)
6 1 Dimostrazione. Sia d 2 = a 2 + b 2 e I a = ρ (P ) (x a) 2 +(y b) 2 d ρ (P ) x 2 + y 2 d + ρ (P ) a 2 + b 2 d 2a ρ (P ) xd 2b ρ (P ) yd I G + md 2 2amx G 2bmy G. (18) Poichè le coordinate del baricentro sono x G = y G =, vale l equazione (17). Osservazione 2 I a I G. Osservazione 3 Fra tutti gli assi paralleli con direzione assegnata, quello passante per il baricentro minimizza il momento d inerzia. Osservazione 4 Se a 1 e a 2 sono due assi paralleli distanti d 1 e d 2 rispettivamente dal baricentro del corpo I a2 = I a1 + m d 2 2 d 2 1. (19) Matrice d Inerzia Scegliamo una terna ortogonale di riferimento con origine O. Sia u il versore dell asse passante per O t.c. u = α i + β j + γ k con α, β e γ coseni direttori rispetto alla terna (O; x, y, z). Scriviamo il momento d inerzia rispetto all asse u I u = r 2 (P ) ρ (P ) d. (2)
7 alcoliamo, attraverso la definizione 11 P O u, corrispondente al vettore r (P ). i j k r (P )= P O u = x y z α β γ = i (yγ zβ) j (xγ zα)+ k (xβ yα) (21) e il suo modulo r (P ) = P O u = P O u sin θ = P O sin θ. (22) alcoliamone il quadrato r 2 (P )= P O u 2 =(yγ zβ) 2 +(xγ zα) 2 +(xβ yα) 2 (23) e sostituiamolo nell espressione (2). Si ottiene I u = ρ (yγ zβ) 2 d + ρ (xγ zα) 2 d + ρ (xβ yα) 2 d = γ 2 ρ y 2 + x 2 d + β 2 ρ x 2 + z 2 d + α 2 ρ z 2 + y 2 d 2αγ ρxzd 2αβ ρxyd 2βγ ρyzd = α 2 I xx + β 2 I yy +γ 2 I zz +2αγI xz +2αβI xy +2βγI yz, (24) dove abbiamo definito i prodotti d inerzia I xz = ρxzd I xy = ρxyd I yz = ρyzd (25) e i momenti d inerzia rispetto agli assi coordinati I xx = ρ (z 2 + y 2 ) d I yy = ρ (x 2 + z 2 ) d I zz = ρ (y 2 + x 2 ) d. (26) Definizione 5 Denotiamo con il simbolo I la matrice d inerzia (o tensore d inerzia) formata dai seguenti elementi I xx I xy I xz I yx I yy I yz. (27) I zx I zy I zz
8 12 Osservazione 5 La quantità espressa dall espressione (2) può essere riscritta nel seguente modo I u =(α, β, γ) I α β = I u u. (28) γ Icoefficienti della matrice I dipendono dalla scelta della terna degli x, y, z. Osservazione 6 Esiste sicuramente almeno una terna rispetto alla quale la matrice I assume una forma diagonale I xx I yy. (29) I zz Questa terna si chiama terna principale d inerzia del corpo relativo al punto O. Osservazione 7 I xx,i yy e I zz sono diversi dagli elementi della matrice (27). Infattisonoimomentid inerziacalcolatirispettoagliassiprincipalid inerziaesono chiamati momenti principali d inerzia. Proprietà 1 Se il corpo ha un piano di simmetria materiale π passante per O è asse principale d inerzia la retta che passa per O perpendicolare al piano. Gli altri due assi vanno cercati nel piano. aso 1 Se il corpo è una figura piana, ogni retta perpendicolare al piano è asse principale d inerzia rispetto al punto O in cui la retta interseca il piano. aso 2 Se il corpo ha due piani di simmetria materiale fra loro ortogonali, per ogni punto della retta d intersezione dei due piani la terna principale d inerzia è costituita dalla retta e dalle due normali. aso 3 Se il corpo è rotondo, ammette piani di simmetria tutti contenenti l asse di rotazione. L asse, quindi, è principale d inerzia e sono principali d inerzia tutti gli assi perpendicolari in O all asse di rotazione (essendo O un qualunque punto dell asse)
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
Integrali doppi - Esercizi svolti
 Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
Integrali doppi - Esercizi svolti Integrali doppi senza cambiamento di variabili Si disegni il dominio e quindi si calcolino gli integrali multipli seguenti:... xy dx dy, con (x, y R x, y x x }; x + y
Proiezioni Grafica 3d
 Proiezioni Grafica 3d Giancarlo RINALDO rinaldo@dipmat.unime.it Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
Proiezioni Grafica 3d Giancarlo RINALDO rinaldo@dipmat.unime.it Dipartimento di Matematica Università di Messina ProiezioniGrafica 3d p. 1 Introduzione Il processo di visualizzazione in 3D è intrinsecamente
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
Prova scritta di Geometria 2 Prof. M. Boratynski
 10/9/2008 Es. 1: Si consideri la forma bilineare simmetrica b su R 3 associata, rispetto alla base canonica {e 1, e 2, e 3 } alla matrice 3 2 1 A = 2 3 0. 1 0 1 1) Provare che (R 3, b) è uno spazio vettoriale
10/9/2008 Es. 1: Si consideri la forma bilineare simmetrica b su R 3 associata, rispetto alla base canonica {e 1, e 2, e 3 } alla matrice 3 2 1 A = 2 3 0. 1 0 1 1) Provare che (R 3, b) è uno spazio vettoriale
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo
 Momento di una forza Nella figura 1 è illustrato come forze uguali e contrarie possono non produrre equilibrio, bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo esteso.
Momento di una forza Nella figura 1 è illustrato come forze uguali e contrarie possono non produrre equilibrio, bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo esteso.
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
Esercizio 2 Si consideri la funzione f definita dalle seguenti condizioni: e x. per x 1 f(x) = α x + e 1 per 1 < x
 FUNZIONI Esercizio 1 Studiare la funzione f(x) = ln ( ) x e disegnarne il grafico. x 1 Esercizio 2 Si consideri la funzione f definita dalle seguenti condizioni: { e x per x 1 f(x) = α x + e 1 per 1
FUNZIONI Esercizio 1 Studiare la funzione f(x) = ln ( ) x e disegnarne il grafico. x 1 Esercizio 2 Si consideri la funzione f definita dalle seguenti condizioni: { e x per x 1 f(x) = α x + e 1 per 1
Dinamica del corpo rigido: Appunti.
 Dinamica del corpo rigido: Appunti. I corpi rigidi sono sistemi di punti materiali, discreti o continui, che hanno come proprietà peculiare quella di conservare la loro forma, oltre che il loro volume,
Dinamica del corpo rigido: Appunti. I corpi rigidi sono sistemi di punti materiali, discreti o continui, che hanno come proprietà peculiare quella di conservare la loro forma, oltre che il loro volume,
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
2 Argomenti introduttivi e generali
 1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Forme bilineari e prodotti scalari. Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione. b :
 Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Lezione del 28-11-2006. Teoria dei vettori ordinari
 Lezione del 8--006 Teoria dei vettori ordinari. Esercizio Sia B = {i, j, k} una base ortonormale fissata. ) Determinare le coordinate dei vettori v V 3 complanari a v =,, 0) e v =, 0, ), aventi lunghezza
Lezione del 8--006 Teoria dei vettori ordinari. Esercizio Sia B = {i, j, k} una base ortonormale fissata. ) Determinare le coordinate dei vettori v V 3 complanari a v =,, 0) e v =, 0, ), aventi lunghezza
Capitolo 16 Esercizi sugli integrali doppi
 Capitolo 6 sercizi sugli integrali doppi Brevi richiami di teoria Sia f : [a, b] [c, d] B IR una funzione limitata e non negativa, definita sul rettangolo R = [a, b] [c, d]. Dividiamo l intervallo [a,
Capitolo 6 sercizi sugli integrali doppi Brevi richiami di teoria Sia f : [a, b] [c, d] B IR una funzione limitata e non negativa, definita sul rettangolo R = [a, b] [c, d]. Dividiamo l intervallo [a,
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
4. Proiezioni del piano e dello spazio
 4. Proiezioni del piano e dello spazio La visualizzazione di oggetti tridimensionali richiede di ottenere una vista piana dell'oggetto. Questo avviene mediante una sequenza di operazioni. Innanzitutto,
4. Proiezioni del piano e dello spazio La visualizzazione di oggetti tridimensionali richiede di ottenere una vista piana dell'oggetto. Questo avviene mediante una sequenza di operazioni. Innanzitutto,
Cambiamento di variabili negli integrali doppi: La trasformazione in coordinate polari. esiste (evidentemente) una sola coppia ( ρ, θ) R [ 0,2π[
 Cambiamento di variabili negli integrali doppi: La trasformazione in coordinate polari Osservazione: Se ( x, ) \{(0,0)} esiste (evidentemente) una sola coppia ( ρ, θ) [ 0,[ tale che x. imane in tal modo
Cambiamento di variabili negli integrali doppi: La trasformazione in coordinate polari Osservazione: Se ( x, ) \{(0,0)} esiste (evidentemente) una sola coppia ( ρ, θ) [ 0,[ tale che x. imane in tal modo
Algebra Lineare e Geometria
 Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
Esame di Geometria - 9 CFU (Appello del 28 gennaio 2013 - A)
 Esame di Geometria - 9 CFU (Appello del 28 gennaio 23 - A) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. Nello spazio R 3, siano dati il piano e i punti P = (, 2, ), Q = (2,, ). π : x + 2y 3
Esame di Geometria - 9 CFU (Appello del 28 gennaio 23 - A) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. Nello spazio R 3, siano dati il piano e i punti P = (, 2, ), Q = (2,, ). π : x + 2y 3
FASCI DI RETTE. scrivere la retta in forma esplicita: 2y = 3x + 4 y = 3 2 x 2. scrivere l equazione del fascio di rette:
 FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
Capitolo 1. Integrali multipli. 1.1 Integrali doppi su domini normali. Definizione 1.1.1 Si definisce dominio normale rispetto all asse
 Contenuti 1 Integrali multipli 2 1.1 Integralidoppisudomininormali... 2 1.2 Cambiamento di variabili in un integrale doppio. 6 1.3 Formula di Gauss-Green nel piano e conseguenze. 7 1.4 Integralitripli...
Contenuti 1 Integrali multipli 2 1.1 Integralidoppisudomininormali... 2 1.2 Cambiamento di variabili in un integrale doppio. 6 1.3 Formula di Gauss-Green nel piano e conseguenze. 7 1.4 Integralitripli...
Calcolo integrale in più variabili
 ppunti di nalisi II Calcolo integrale in più variabili Integrali doppi Nel caso di una funzione di una variabile f : a, b] R, supponendo f continua e fx) a, b], la quantità b a fx)dx indica l area fra
ppunti di nalisi II Calcolo integrale in più variabili Integrali doppi Nel caso di una funzione di una variabile f : a, b] R, supponendo f continua e fx) a, b], la quantità b a fx)dx indica l area fra
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
6. Calcolare le derivate parziali prime e seconde, verificando la validità del teorema di Schwarz:
 FUNZIONI DI PIU VARIABILI Esercizi svolti. Determinare il dominio delle seguenti funzioni e rappresentarlo graficamente : (a) f log( x y ) (b) f log(x + y ) (c) f y x 4 (d) f sin(x + y ) (e) f log(xy +
FUNZIONI DI PIU VARIABILI Esercizi svolti. Determinare il dominio delle seguenti funzioni e rappresentarlo graficamente : (a) f log( x y ) (b) f log(x + y ) (c) f y x 4 (d) f sin(x + y ) (e) f log(xy +
Le trasformazioni geometriche
 Le trasformazioni geometriche Le trasformazioni geometriche Le trasformazioni affini del piano o affinità Le similitudini Le isometrie Le traslazioni Le rotazioni Le simmetrie assiale e centrale Le omotetie
Le trasformazioni geometriche Le trasformazioni geometriche Le trasformazioni affini del piano o affinità Le similitudini Le isometrie Le traslazioni Le rotazioni Le simmetrie assiale e centrale Le omotetie
Rette e piani con le matrici e i determinanti
 CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Massimi e minimi vincolati di funzioni in due variabili
 Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
09 - Funzioni reali di due variabili reali
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 09 - Funzioni reali di due variabili reali Anno Accademico 2013/2014
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 09 - Funzioni reali di due variabili reali Anno Accademico 2013/2014
Processo di rendering
 Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Analisi Matematica di circuiti elettrici
 Analisi Matematica di circuiti elettrici Eserciziario A cura del Prof. Marco Chirizzi 2011/2012 Cap.5 Numeri complessi 5.1 Definizione di numero complesso Si definisce numero complesso un numero scritto
Analisi Matematica di circuiti elettrici Eserciziario A cura del Prof. Marco Chirizzi 2011/2012 Cap.5 Numeri complessi 5.1 Definizione di numero complesso Si definisce numero complesso un numero scritto
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
SOLUZIONE DEL PROBLEMA 2 CORSO DI ORDINAMENTO 2013. 8 4 + x 2, con dominio R (infatti x2 + 4 0 per ogni. 8 4 + ( x) = 8. 4 + x 2
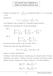 SOLUZIONE DEL PROBLEMA CORSO DI ORDINAMENTO. Studiamo la funzione f(x) = x R). Notiamo che f( x) = 4 + x, con dominio R (infatti x + 4 per ogni 4 + ( x) = 4 + x = f(x), cioè la funzione è pari e il grafico
SOLUZIONE DEL PROBLEMA CORSO DI ORDINAMENTO. Studiamo la funzione f(x) = x R). Notiamo che f( x) = 4 + x, con dominio R (infatti x + 4 per ogni 4 + ( x) = 4 + x = f(x), cioè la funzione è pari e il grafico
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica Terzo Appello del corso di Geometria e Algebra II Parte - Docente F. Flamini, Roma, 7/09/2007 SVOLGIMENTO COMPITO III APPELLO
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Elettronica Terzo Appello del corso di Geometria e Algebra II Parte - Docente F. Flamini, Roma, 7/09/2007 SVOLGIMENTO COMPITO III APPELLO
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Liceo G.B. Vico Corsico
 Liceo G.B. Vico Corsico Classe: 3A Materia: MATEMATICA Insegnante: Nicola Moriello Testo utilizzato: Bergamini Trifone Barozzi: Manuale blu.0 di Matematica Moduli S, L, O, Q, Beta ed. Zanichelli 1) Programma
Liceo G.B. Vico Corsico Classe: 3A Materia: MATEMATICA Insegnante: Nicola Moriello Testo utilizzato: Bergamini Trifone Barozzi: Manuale blu.0 di Matematica Moduli S, L, O, Q, Beta ed. Zanichelli 1) Programma
Esercizi svolti sui numeri complessi
 Francesco Daddi - ottobre 009 Esercizio 1 Risolvere l equazione z 1 + i = 1. Soluzione. Moltiplichiamo entrambi i membri per 1 + i in definitiva la soluzione è z 1 + i 1 + i = 1 1 + i z = 1 1 i. : z =
Francesco Daddi - ottobre 009 Esercizio 1 Risolvere l equazione z 1 + i = 1. Soluzione. Moltiplichiamo entrambi i membri per 1 + i in definitiva la soluzione è z 1 + i 1 + i = 1 1 + i z = 1 1 i. : z =
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Punti notevoli di un triangolo
 Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Anno 5 4. Funzioni reali: il dominio
 Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
Anno 5 4 Funzioni reali: il dominio 1 Introduzione In questa lezione impareremo a definire cos è una funzione reale di variabile reale e a ricercarne il dominio. Al termine di questa lezione sarai in grado
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
A.1 Definizione e rappresentazione di un numero complesso
 441 APPENDICE A4 NUMERI COMPLESSI A.1 Definizione e rappresentazione di un numero complesso Si riepilogano i concetti e le operazioni elementari relativi ai numeri complessi. Sia z un numero complesso;
441 APPENDICE A4 NUMERI COMPLESSI A.1 Definizione e rappresentazione di un numero complesso Si riepilogano i concetti e le operazioni elementari relativi ai numeri complessi. Sia z un numero complesso;
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
LA RETTA. b) se l equazione si presente y=mx+q (dove q è un qualsiasi numero reale) si ha una retta generica del piano.
 LA RETTA DESCRIZIONE GENERALE Nella GEOMETRIA ANALITICA si fa sempre un riferimento rispetto al piano cartesiano Oxy; questa riguarda lo studio della retta, delle trasformazioni lineari piane e delle coniche.
LA RETTA DESCRIZIONE GENERALE Nella GEOMETRIA ANALITICA si fa sempre un riferimento rispetto al piano cartesiano Oxy; questa riguarda lo studio della retta, delle trasformazioni lineari piane e delle coniche.
Esercizi di riepilogo Matematica II Corso di Laurea in Ottica ed Optometria
 Esercizi di riepilogo Matematica II Corso di Laurea in Ottica ed Optometria Esercizio 1 Testo Sia F F 1 x,y),f x,y)) ) x 1 x y + 1 x, y 1 x y + 1 y un campo vettoriale. 1. Si determini il dominio in cui
Esercizi di riepilogo Matematica II Corso di Laurea in Ottica ed Optometria Esercizio 1 Testo Sia F F 1 x,y),f x,y)) ) x 1 x y + 1 x, y 1 x y + 1 y un campo vettoriale. 1. Si determini il dominio in cui
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Energia potenziale L. P. Maggio 2007. 1. Campo di forze
 Energia potenziale L. P. Maggio 2007 1. Campo di forze Consideriamo un punto materiale di massa m che si muove in una certa regione dello spazio. Si dice che esso è soggetto a un campo di forze, se ad
Energia potenziale L. P. Maggio 2007 1. Campo di forze Consideriamo un punto materiale di massa m che si muove in una certa regione dello spazio. Si dice che esso è soggetto a un campo di forze, se ad
Maturità Scientifica PNI, sessione ordinaria 2000-2001
 Matematica per la nuova maturità scientifica A. Bernardo M. Pedone Maturità Scientifica PNI, sessione ordinaria 000-00 Problema Sia AB un segmento di lunghezza a e il suo punto medio. Fissato un conveniente
Matematica per la nuova maturità scientifica A. Bernardo M. Pedone Maturità Scientifica PNI, sessione ordinaria 000-00 Problema Sia AB un segmento di lunghezza a e il suo punto medio. Fissato un conveniente
2. Giovedì 5/03/2015, 11 13. ore: 2(4) Spazi vettoriali euclidei. Vettori nello spazio fisico: Prodotto scalare e prodotto
 Registro delle lezioni di MECCANICA 1 Corso di Laurea in Matematica 8 CFU - A.A. 2014/2015 docente: Francesco Demontis ultimo aggiornamento: 21 maggio 2015 1. Lunedì 2/03/2015, 11 13. ore: 2(2) Presentazione
Registro delle lezioni di MECCANICA 1 Corso di Laurea in Matematica 8 CFU - A.A. 2014/2015 docente: Francesco Demontis ultimo aggiornamento: 21 maggio 2015 1. Lunedì 2/03/2015, 11 13. ore: 2(2) Presentazione
Sia data la rete di fig. 1 costituita da tre resistori,,, e da due generatori indipendenti ideali di corrente ed. Fig. 1
 Analisi delle reti 1. Analisi nodale (metodo dei potenziali dei nodi) 1.1 Analisi nodale in assenza di generatori di tensione L'analisi nodale, detta altresì metodo dei potenziali ai nodi, è un procedimento
Analisi delle reti 1. Analisi nodale (metodo dei potenziali dei nodi) 1.1 Analisi nodale in assenza di generatori di tensione L'analisi nodale, detta altresì metodo dei potenziali ai nodi, è un procedimento
Richiami sulle derivate parziali e definizione di gradiente di una funzione, sulle derivate direzionali. Regola della catena per funzioni composte.
 PROGRAMMA di Fondamenti di Analisi Matematica 2 (che sarà svolto fino al 7 gennaio 2013) A.A. 2012-2013, Paola Mannucci e Claudio Marchi, Canali 1 e 2 Ingegneria Gestionale, Meccanica-Meccatronica, Vicenza
PROGRAMMA di Fondamenti di Analisi Matematica 2 (che sarà svolto fino al 7 gennaio 2013) A.A. 2012-2013, Paola Mannucci e Claudio Marchi, Canali 1 e 2 Ingegneria Gestionale, Meccanica-Meccatronica, Vicenza
Integrali di superficie: esercizi svolti
 Integrali di superficie: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio. Calcolare i seguenti integrali superficiali sulle superfici
Integrali di superficie: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio. Calcolare i seguenti integrali superficiali sulle superfici
QUANTITÀ DI MOTO E MOMENTO DELLA QUANTITÀ DI MOTO
 QUANTITÀ DI MOTO E MOMENTO DELLA QUANTITÀ DI MOTO Quantità di Moto Definizione 1 Per un punto P dotato di massa m e velocità v, sidefinisce quantità di moto il seguente vettore Q := m v. (1) Definizione
QUANTITÀ DI MOTO E MOMENTO DELLA QUANTITÀ DI MOTO Quantità di Moto Definizione 1 Per un punto P dotato di massa m e velocità v, sidefinisce quantità di moto il seguente vettore Q := m v. (1) Definizione
Unità Didattica N 28 Punti notevoli di un triangolo
 68 Unità Didattica N 8 Punti notevoli di un triangolo Unità Didattica N 8 Punti notevoli di un triangolo 0) ircocentro 0) Incentro 03) Baricentro 04) Ortocentro Pagina 68 di 73 Unità Didattica N 8 Punti
68 Unità Didattica N 8 Punti notevoli di un triangolo Unità Didattica N 8 Punti notevoli di un triangolo 0) ircocentro 0) Incentro 03) Baricentro 04) Ortocentro Pagina 68 di 73 Unità Didattica N 8 Punti
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
GEOMETRIA I Corso di Geometria I (seconda parte)
 Corso di Geometria I (seconda parte) anno acc. 2009/2010 Cambiamento del sistema di riferimento in E 3 Consideriamo in E 3 due sistemi di riferimento ortonormali R e R, ed un punto P (x, y, z) in R. Lo
Corso di Geometria I (seconda parte) anno acc. 2009/2010 Cambiamento del sistema di riferimento in E 3 Consideriamo in E 3 due sistemi di riferimento ortonormali R e R, ed un punto P (x, y, z) in R. Lo
Laboratorio di Rappresentazione e Modellazione dell Architettura
 Laboratorio di Rappresentazione e Modellazione dell Architettura Seconda Università di Napoli Facoltà di Architettura Corso di Laurea in Architettura Laboratorio di Rappresentazione e Modellazione dell
Laboratorio di Rappresentazione e Modellazione dell Architettura Seconda Università di Napoli Facoltà di Architettura Corso di Laurea in Architettura Laboratorio di Rappresentazione e Modellazione dell
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Esercizi svolti e assegnati su integrali doppi e tripli
 Esercizi svolti e assegnati su integrali doppi e tripli Esercizio. ove R R xy x + y + x + y dxdy } x, y R : x, y, x x + y x Svolgimento. Passo : per disegnare R, studiamo C : x + y x, C : x + y x Completando
Esercizi svolti e assegnati su integrali doppi e tripli Esercizio. ove R R xy x + y + x + y dxdy } x, y R : x, y, x x + y x Svolgimento. Passo : per disegnare R, studiamo C : x + y x, C : x + y x Completando
Università di Trieste Facoltà d Ingegneria. Esercizi sul calcolo differenziale in IR N. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria Esercizi sul calcolo differenziale in IR N Dott Franco Obersnel Esercizio 1 Si calcoli la derivata direzionale nell origine lungo la direzione y del versore v
Università di Trieste Facoltà d Ingegneria Esercizi sul calcolo differenziale in IR N Dott Franco Obersnel Esercizio 1 Si calcoli la derivata direzionale nell origine lungo la direzione y del versore v
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
FAM. 1. Sistema composto da quattro PM come nella tabella seguente
 Serie 11: Meccanica IV FAM C. Ferrari Esercizio 1 Centro di massa: sistemi discreti Determina il centro di massa dei seguenti sistemi discreti. 1. Sistema composto da quattro PM come nella tabella seguente
Serie 11: Meccanica IV FAM C. Ferrari Esercizio 1 Centro di massa: sistemi discreti Determina il centro di massa dei seguenti sistemi discreti. 1. Sistema composto da quattro PM come nella tabella seguente
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.
![x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario. x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.](/thumbs/39/18585741.jpg) Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
1 Introduzione alla Meccanica Razionale 1 1.1 Che cos è la Meccanica Razionale... 1 1.2 Un esempio... 2
 Indice 1 Introduzione alla Meccanica Razionale 1 1.1 Che cos è la Meccanica Razionale..................... 1 1.2 Un esempio................................. 2 2 Spazi Vettoriali, Spazio e Tempo 7 2.1 Cos
Indice 1 Introduzione alla Meccanica Razionale 1 1.1 Che cos è la Meccanica Razionale..................... 1 1.2 Un esempio................................. 2 2 Spazi Vettoriali, Spazio e Tempo 7 2.1 Cos
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
FM210 - Fisica Matematica I
 FM10 - Fisica Matematica I Seconda Prova di Esonero [13-01-01] Soluzioni Problema 1 1. Il moto si svolge in un campo di forze centrale in assenza di attrito. Pertanto si avranno due integrali primi del
FM10 - Fisica Matematica I Seconda Prova di Esonero [13-01-01] Soluzioni Problema 1 1. Il moto si svolge in un campo di forze centrale in assenza di attrito. Pertanto si avranno due integrali primi del
Anno 5 Funzioni inverse e funzioni composte
 Anno 5 Funzioni inverse e funzioni composte 1 Introduzione In questa lezione impareremo a definire e ricercare le funzioni inverse e le funzioni composte. Al termine di questa lezione sarai in grado di:
Anno 5 Funzioni inverse e funzioni composte 1 Introduzione In questa lezione impareremo a definire e ricercare le funzioni inverse e le funzioni composte. Al termine di questa lezione sarai in grado di:
I numeri complessi. Mario Spagnuolo Corso di Laurea in Fisica - Facoltà di Scienze - Università Federico II di Napoli
 I numeri complessi Mario Spagnuolo Corso di Laurea in Fisica - Facoltà di Scienze - Università Federico II di Napoli 1 Introduzione Studiare i numeri complessi può sembrare inutile ed avulso dalla realtà;
I numeri complessi Mario Spagnuolo Corso di Laurea in Fisica - Facoltà di Scienze - Università Federico II di Napoli 1 Introduzione Studiare i numeri complessi può sembrare inutile ed avulso dalla realtà;
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
 1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
Funzioni di più variabili. Ottimizzazione libera e vincolata
 libera e vincolata Generalità. Limiti e continuità per funzioni di 2 o Piano tangente. Derivate successive Formula di Taylor libera vincolata Lo ordinario è in corrispondenza biunivoca con i vettori di
libera e vincolata Generalità. Limiti e continuità per funzioni di 2 o Piano tangente. Derivate successive Formula di Taylor libera vincolata Lo ordinario è in corrispondenza biunivoca con i vettori di
a t Esercizio (tratto dal problema 5.10 del Mazzoldi)
 1 Esercizio (tratto dal problema 5.10 del Mazzoldi) Una guida semicircolare liscia verticale di raggio = 40 cm è vincolata ad una piattaforma orizzontale che si muove con accelerazione costante a t = 2
1 Esercizio (tratto dal problema 5.10 del Mazzoldi) Una guida semicircolare liscia verticale di raggio = 40 cm è vincolata ad una piattaforma orizzontale che si muove con accelerazione costante a t = 2
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
M P = PA^V. Il risultante e denito semplicemente come la somma dei vettori di a
 VETTORI APPLICATI Sistema di vettori applicati L'ente matematico costituito da un punto P e da un vettore (libero) V, si dice vettore applicato in P e si denota con (P;V). E comodo rappresentare il vettore
VETTORI APPLICATI Sistema di vettori applicati L'ente matematico costituito da un punto P e da un vettore (libero) V, si dice vettore applicato in P e si denota con (P;V). E comodo rappresentare il vettore
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti];
![1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti]; 1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti];](/thumbs/24/2314490.jpg) 1 Esercizio Una ruota di raggio R = 15 cm e di massa M = 8 Kg può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2 = 30 0, ed è collegato tramite un filo inestensibile ad un blocco di
1 Esercizio Una ruota di raggio R = 15 cm e di massa M = 8 Kg può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2 = 30 0, ed è collegato tramite un filo inestensibile ad un blocco di
Università degli studi di Salerno corso di studi in Ingegneria Informatica TUTORATO DI FISICA. Lezione 5 - Meccanica del punto materiale
 Università degli studi di Salerno corso di studi in Ingegneria Informatica TUTORATO DI FISICA Esercizio 1 Lezione 5 - Meccanica del punto materiale Un volano è costituito da un cilindro rigido omogeneo,
Università degli studi di Salerno corso di studi in Ingegneria Informatica TUTORATO DI FISICA Esercizio 1 Lezione 5 - Meccanica del punto materiale Un volano è costituito da un cilindro rigido omogeneo,
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
1 Definizione: lunghezza di una curva.
 Abstract Qui viene affrontato lo studio delle curve nel piano e nello spazio, con particolare interesse verso due invarianti: la curvatura e la torsione Il primo ci dice quanto la curva si allontana dall
Abstract Qui viene affrontato lo studio delle curve nel piano e nello spazio, con particolare interesse verso due invarianti: la curvatura e la torsione Il primo ci dice quanto la curva si allontana dall
FOGLIO 6 - Esercizi Riepilogativi Svolti. Nei seguenti esercizi, si consideri fissato una volta per tutte un riferimento proiettivo per
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Edile/Architettura Esercizi per il corso di GEOMETRIA 2 - aa 2007/2008 Docente: Prof F Flamini - Tutore: Dott M Paganin FOGLIO 6 - Esercizi
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Edile/Architettura Esercizi per il corso di GEOMETRIA 2 - aa 2007/2008 Docente: Prof F Flamini - Tutore: Dott M Paganin FOGLIO 6 - Esercizi
Geometria analitica di base (prima parte)
 SAPERE Al termine di questo capitolo, avrai appreso: come fissare un sistema di riferimento cartesiano ortogonale il significato di equazione di una retta il significato di coefficiente angolare di una
SAPERE Al termine di questo capitolo, avrai appreso: come fissare un sistema di riferimento cartesiano ortogonale il significato di equazione di una retta il significato di coefficiente angolare di una
4. Operazioni binarie, gruppi e campi.
 1 4. Operazioni binarie, gruppi e campi. 4.1 Definizione. Diremo - operazione binaria ovunque definita in A B a valori in C ogni funzione f : A B C - operazione binaria ovunque definita in A a valori in
1 4. Operazioni binarie, gruppi e campi. 4.1 Definizione. Diremo - operazione binaria ovunque definita in A B a valori in C ogni funzione f : A B C - operazione binaria ovunque definita in A a valori in
