Dipendenza dai dati iniziali
|
|
|
- Sofia Russo
- 8 anni fa
- Visualizzazioni
Transcript
1 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono dai dati iniziali. Denotando con y 0 (t) la soluzione dell equazione differenziale y = f(t, y) con dati iniziali y( ) = y 0, se interpretiamo la traiettoria come l evoluzione nel tempo del nostro sistema fisico, ci aspettiamo che variando di poco la posizione iniziale y 0 (o il tempo iniziale ) la traiettoria della corrispondente soluzione sia vicina a quella di y 0 (t). Più precisamente, se y 1 (t) denota la soluzione della medesi- y y 0 (t) (,y 0 ) y 1 (t) (,z 0 ) Ω t Figura 1: Confronto tra soluzioni ma equazione differenziale e tale che y 1 ( ) = y 1 ci aspettiamo che quando y 1 è vicino a y 0 le traiettorie di y 0 (t) e y 1 (t) siano vicine, e se y 1 tende a y 0 ci aspettiamo che le due traiettorie tendano a sovrapporsi, ovvero ci sia una qualche continuità delle soluzioni dai dati iniziali (a volte chiamata anche stability ). In questo capitolo studieremo come le soluzioni dipendono da e y 0, e vedremo che, sotto le usuali ipotesi per f, la mappa che associa al dato y 0 la soluzione che assume tale dato al tempo è continua e differen- 1
2 2 DIPENDENZA DAI DATI INIZIALI ziabile. Analizzeremo infine anche la dipendenza delle soluzioni dal tempo iniziale e dal campo vettoriale f. Dipendenza continua dai dati iniziali In questa sezione dimostreremo la continuità delle soluzioni di un equazione differenziale dal dato iniziale y 0. Chiaramente, se le soluzioni dei problemi di Cauchy non sono uniche a maggior ragione perde anche senso parlare di dipendenza continua dai dati iniziali. Di conseguenza, se non diversamente specificato, d ora in avanti assumeremo l unicità delle soluzioni dei problemi di Cauchy relativi all equazione differenziale in considerazione. Sappiamo che ciò garantisce l esistenza di un unica soluzione massimale per ciascuno di tali problemi. Per evidenziare la dipendenza della soluzione dai dati iniziali, nel seguito denoteremo con y(t;, y 0 ) la soluzione (massimale) del problema di Cauchy (1) y = f(t, y) y( ) = y 0. Nel caso in cui il tempo iniziale sia fissato, per concentrarci sulla sola dipendenza della soluzione dal dato iniziale y 0 useremo anche la notazione ridotta y(t; y 0 ). Vediamo ora che nel caso in cui valgono le ipotesi del Teorema di Cauchy-Lipschitz, la dipendenza della soluzione dai dati iniziali è addirittura lipschitziana. Teorema 1 (di dipendenza continua dai dati (I)) Sia f : Ω R R n R n continua e localmente lipschitziana (rispetto alle variabili y). Allora i) per ogni (, y 0 ), (, z 0 ) Ω esistono δ > 0, C > 0 tali che (2) y( ; y0 ) y( ; z 0 ) C y 0 z 0, dove si è posto y( ; y 0 ) y( ; z 0 ) = sup t Iδ ( ) y(t; y 0 ) y(t; z 0 ) ; ii) più in generale, fissato un compatto K Ω esistono δ, C > 0 (dipendenti solo da K e f) tali che per ogni (, y 0 ), (, z 0 ) K vale (2). In altri termini, l applicazione y 0 y( ; y 0 ) è localmente lipschitziana come funzione da R n in ( C(I δ, R n ), ).
3 DIPENDENZA CONTINUA DAI DATI INIZIALI 3 Dimostrazione i) Presi (, y 0 ), (, z 0 ) Ω denotiamo con I e I gli intervalli di definizione, rispettivamente, di y(t; y 0 ) e y(t; z 0 ). Sia K un compatto che contiene le due traiettorie ristrette all intervallo I I (per esempio, se I I è chiuso, l unione delle traiettorie medesime) e sia L la costante di Lipschitz di f in K. Si prenda infine δ tale che δl < 1. Come nella dimostrazione del Teorema di Cauchy, per t I δ ( ) I I si ottiene (3) y(t; y0 ) y(t; z 0 ) t = y 0 z 0 + f(s, y(s; y 0 )) f(s, y(s; z 0 )) ds t y 0 z 0 + f(s, y(s; y 0 )) f(s, y(s; z 0 )) ds t y 0 z 0 + L y(s; y 0 ) y(s; z 0 ) ds y 0 z 0 + δl y( ; y0 ) y( ; z 0 ). Passando all estremo superiore sui t I δ e riordinando i termini si ottiene y( ; y 0 ) y( ; z 0 ) 1 1 δl y 0 z 0, da cui la tesi con C = (1 δl) 1. ii) Nel punto precedente si è visto come le costanti δ, C dipendono da y 0 e z 0. Verifichiamo che è possibile prenderle uniformi in un compatto contenente (, y 0 ) e (, z 0 ) (ciò è necessario per potere far tendere in seguito z 0 a y 0 e ottenere la lipschitzianità). Fissato un compatto K in Ω, sia C α,r (K) Ω definito come in (12) nella dimostrazione del Teorema 12 di Peano sui compatti. Per quest ultimo teorema e per il Lemma 3.19 delle dispense ogni soluzione massimale con dati iniziali (, y 0 ) in K è definita almeno in I ε ( ) con ε = minα, R/M K }, essendo M K il massimo della norma di f in C α,r (K); inoltre, per il Lemma 2.8 delle dispense la traiettoria di y(t; y 0 ), t I ε ( ), è contenuta in C ε,r (, y 0 ) C α,r (K) che è dunque un compatto contenente tutte le traiettorie al variare di (, y 0 ) K. Sia infine L la costante di Lipschitz di f in C α,r (K) e come prima si prenda δ tale che δ ε e δl < 1. Con queste scelte di L, δ le stime (3) continuano a valere per ogni t I δ ( ), uniformemente per ogni (, y 0 ), (, z 0 ) K, da cui la tesi. Del teorema precedente segue che la traiettoria di y(t; z 0 ) converge uniformemente a quella di y(t; y 0 ) quando z 0 tende a y 0. Esercizio 2 Generalizzare il teorema precedente al caso in cui anche può variare; più precisamente, definiti C α,r (K) e M K come nella dimostrazione
4 4 DIPENDENZA DAI DATI INIZIALI del Teorema 12, si verifichi che esistono δ, C > 0 tali che (4) y( ;, y 0 ) y( ; t 1, y 1 ) C [ M K t 1 + y 0 y 1 ]. Le disuguaglianze (2) e (4) forniscono una stima sulla norma infinito della distanza tra due soluzioni; quest ultima implica banalmente la disuguaglianza puntuale y(t; y 0 ) y(t; z 0 ) C y 0 z 0, per ogni t I δ ( ). Si osservi che quest ultima non è ottimale in quanto per t = si ottiene y 0 z 0 < C y 0 z 0, con C = (1 δl) 1 > 1. Volendo ottenere una stima puntuale più precisa si può utilizzare il Lemma di Gronwall, un classico strumento nell ambito delle equazioni differenziali, utilissimo per esempio per dimostrare l unicità delle soluzioni e per ottenere stime sulle medesime. Fornisce inoltre un primo approccio alle cosiddette disequazioni integrali e, per certi aspetti, è l equivalente del Teorema del confronto 5.1 delle dispense (quest ultimo può anche essere utilizzato proprio per dimostrare il Lemma). Lemma 3 (di Gronwall) Sia v : I R continua e non negativa tale che esistano α, β 0, I per cui t (5) v(t) α + β v(s) ds. Allora (6) v(t) αe β t. Osservazione 4 La differenza fondamentale tra (5) e (6) sta nel fatto che nella prima la funzione v(t) compare sia a destra che a sinistra della disuguaglianza, nella seconda compare solo a sinistra e quindi fornisce un effettiva stima di v(t). Dimostrazione (del Lemma di Gronwall) Verifichiamo la tesi nel caso t >, cioè in futuro, nel qual caso si può togliere il valore assoluto sia in (5) che in (6). Introdotta la funzione u(t) := α + β t v(s) ds, per ipotesi si ha v(t) u(t) per ogni t >. Inoltre d ( u(t)e β(t ) ) ( ( = βe β(t ) v(t) α + β dt t )) v(s) ds 0,
5 DIPENDENZA CONTINUA DAI DATI INIZIALI 5 ovvero la funzione w(t) = u(t)e β(t ) è decrescente per t, dunque w(t) w( ) = α da cui v(t)e β(t ) u(t)e β(t ) α, cioè la tesi per t. Alternativamente si può utilizzare il Teorema del confronto 5.4 delle dispense. Anche qui verifichiamo la tesi nel caso t >, cioè in futuro. Introdotta la funzione u(t) come sopra, per ipotesi si ha v(t) u(t) per ogni t >. È dunque sufficiente dimostrare che la tesi vale per u cioè che u(t) αe β(t t0) per t >. Per ipotesi u è derivabile e si ha u (t) = βv(t) βu(t), per ogni t >. In particolare u(t) è sottosoluzione in futuro per la soluzione del problema di Cauchy z = βz z( ) = u( ) = α. Essendo tale soluzione data da z(t) = αe β(t ), per il Teorema del confronto 5.4 delle dispense si ottiene u(t) z(t) per t >, da cui la tesi. Per esercizio, si verifichi (utilizzando il Teorema del confronto o facendo un calcolo diretto) che la tesi vale anche in passato, cioè per t <. Grazie al Lemma di Gronwall è possibile ottenere un generalizzazione del Teorema 1. Teorema 5 (di dipendenza continua dai dati (II)) Sia f : Ω R R n R n continua e localmente lipschitziana (rispetto alle variabili y). Dati (, y 0 ), (, z 0 ) Ω allora (7) y(t; y 0 ) y(t; z 0 ) e L t t0 y 0 z 0, per ogni t in un comune intervallo di definizione I δ, dove L è la costante di Lipschitz di f in un compatto che contiene entrambe le traiettorie. Inoltre è possibile prendere L, δ uniformi per (, y 0 ), (, z 0 ) che variano in un compatto di Ω. Dimostrazione Fissato un compatto K che contiene entrambe le traiettorie e detta L la costante di Lipschitz di f in K, operando come in (3), per ogni t I δ si ottiene y(t; y 0 ) y(t; z 0 ) t y 0 z 0 + L y(s; y 0 ) y(s; z 0 ) ds.
6 6 DIPENDENZA DAI DATI INIZIALI Applicando il Lemma di Gronwall alla funzione v(t) = y(t; y 0 ) y(t; z 0 ) con α = y 0 z 0 e β = L si ottiene la tesi. La generalizzazione per dati che variano in un compatto di Ω si ottiene analogamente alla dimostrazione del punto ii) del Teorema 1. Uno dei punti deboli dei Teoremi 1 e 5 è che permettono di confrontare le soluzioni solamente su un piccolo intorno di, mentre le soluzioni in origine potrebbero essere definite su intervalli possibilmente molto grandi. Si confrontino questi risultati con quelli ottenuti nei Teoremi 10 e 11 dove le soluzioni vengono confrontate con una soluzione su un dominio compatto fissato a priori (si veda anche il Teorema 9.5 delle dispense). Esercizio 6 Generalizzare il teorema precedente al caso in cui anche può variare; più precisamente, definiti C α,r (K) e M = M K come nella dimostrazione del Teorema 12, si verifichi che esistono δ, L > 0 tali che (8) y(t;, y 0 ) y(t; t 1, y 1 ) e L t [ M t 1 + y 0 y 1 ]. Esercizio 7 Utilizzando il Lemma di Gronwall, dimostrare il teorema di unicità delle soluzioni per i problemi di Cauchy associati a y = f(t, y) nel caso in cui f sia localmente lipschitziana rispetto alle variabili y. Differenziabilità rispetto ai dati iniziali Analogamente alla continuità, si può anche studiare la differenziabilità della mappa y 0 y( ; y 0 ). Supponendo di aver già dimostrato la differenziabilità di tale mappa, derivando parzialmente l equazione y = f(t, y) rispetto alle variabili y 0, dovrà allora essere ( d ) D y0 dt y(t; y ( 0) = D y0 f(t, y(t; y0 )) ) = D y f(t, y(t; y 0 ))D y0 y(t; y 0 ). Potendo scambiare l ordine di derivazione si ottiene d ( Dy0 y(t; y 0 ) ) = D y f(t, y(t; y 0 ))D y0 y(t; y 0 ), dt ovvero l applicazione D y0 y( ; y 0 ) : R L(R n, R n ) M(n) è soluzione dell equazione differenziale lineare in forma matriciale Y = D y f(t, y(t; y 0 ))Y. Per quanto concerne il dato iniziale si ha D y0 ( y(t0 ; y 0 ) ) = D y0 y 0 = I, dove I è l identità. In effetti, si può dimostrare il seguente risultato.
7 DIPENDENZA CONTINUA RISPETTO AL CAMPO VETTORIALE 7 Teorema 8 (di differenziabilità rispetto ai dati) Sia f : Ω R n, con Ω R R n aperto, continua e con derivate parziali rispetto a y continue. Allora la mappa y 0 y(t; y 0 ) è differenziabile e l applicazione t D y0 y(t; y 0 ) da R in M(n) è la soluzione al tempo t del problema di Cauchy in forma matriciale Y = D y f(t, y(t; y 0 ))Y (9) Y ( ) = I, dove y(t; y 0 ) è la soluzione di (1). Dimostrazione Omessa (si può ottenere mediante un opportuna generalizzazione del Lemma di Gronwall). Dipendenza continua rispetto al campo vettoriale Il Lemma di Gronwall permette anche di dimostrare un risultato di continuità delle soluzioni di un equazione differenziale rispetto al campo vettoriale. Premettiamo il seguente risultato preliminare al risultato più generale dato dal Teorema 10. Teorema 9 (di Kamke) Siano f, g : Ω R n, Ω R R n aperto, funzioni continue e localmente lipschitziane rispetto alla variabile y. Fissati (, y 0 ), (s 0, z 0 ) Ω, sia y : I R n la soluzione in I = [ δ 0, + δ 0 ] del problema di Cauchy y = f(t, y) y( ) = y 0, e sia z : J R n la soluzione in J = [s 0 δ 0, s 0 +δ 0 ] del problema di Cauchy z = g(t, z) z(s 0 ) = z 0. Allora esistono costanti positive ε = ε(, g), M = M g (K), L = L f (K), d = d(δ 0, δ 0 ), dove K Ω è un compatto che contiene le traiettorie di y(t) e z(t) ristrette a I J, tali che se s 0 ε si ha (10) y(t) z(t) [ y 0 z 0 + M s 0 + d f g ] e L t, per ogni t I J, dove si è posto f g := max (τ,x) K f(τ, x) g(τ, x).
8 8 DIPENDENZA DAI DATI INIZIALI Dimostrazione Fissati (, y 0 ) e la relativa soluzione y(t) in I, se s 0 è sufficientemente vicino a si avrà s 0 I e J, in particolare l intervallo di estremi e s 0 sarà contenuto in I J che quindi sarà non vuoto. In realtà dobbiamo anche applicare il Teorema di Peano sui compatti per garantire l esistenza di un intervallo di definizione comune per tutte le corrispondenti soluzioni z(t) al variare di (s 0, z 0 ) in un intorno compatto di (, z 0 ). Più precisamente, si prende ε uguale all ε K del Teorema 12 relativo al compatto K = I z 0 } e alla funzione g. Sia K un qualsiasi compatto contenuto in Ω e contenente le traiettorie di y(t) e z(t) ristrette a I J (per esempio si potrebbe prendere K proprio uguale all unione di queste due traiettorie), si definiscano M = M g (K) := max (s,z) K g(s, z), d = d(δ 0, δ 0) = ampiezza di I J, e sia L la costante di Lipschitz di f(t, ) sul compatto K. Si ha y(t) z(t) = y 0 + da cui segue t f(s, y(s)) ds s0 ( z 0 + t ) g(s, z(s)) ds s 0 t ( ) = y 0 z 0 + g(s, z(s)) ds + f(s, z(s)) g(s, z(s)) ds + t ( ) + f(s, y(s)) f(s, z(s)) ds, y(t) z(t) t0 t y 0 z 0 + g(s, z(s)) ds + f(s, z(s)) g(s, z(s)) ds + s 0 t + f(s, y(s)) f(s, z(s)) ds t y 0 z 0 + M s 0 + d f g + L y(s) z(s) ds. A questo punto si può applicare il Lemma di Gronwall alla funzione v(t) = y(t) z(t) : I J R, con α = y 0 z 0 + M s 0 + d f g e β = L, ottenendo (10). Dal Teorema di Kamke si deduce che la distanza tra le soluzioni di due problemi di Cauchy cresce al più esponenzialmente rispetto alla loro distanza iniziale misurata in termini della distanza tra i dati iniziali e tra i campi vettoriali. Come corollario si dimostra il seguente risultato.
9 DIPENDENZA CONTINUA RISPETTO AL CAMPO VETTORIALE 9 Teorema 10 (di Kamke, di dipendenza continua dai dati (III)) Siano date f, f k : Ω R R n R n, k = 1, 2,..., continue e localmente lipschitziane rispetto alla variabile y, e siano dati (t k, y k ) Ω per k N. Denotiamo con y(t) la soluzione nell intervallo chiuso e limitato I del problema di Cauchy y = f(t, y) y( ) = y 0. Se (t k, y k ) (, y 0 ) e f k f per k + uniformemente sui compatti di Ω, detta y k (t) la soluzione del problema di Cauchy y = f k (t, y) y(t k ) = y k, definitivamente per k k la funzione y k (t) può essere definita in I e si ha y k (t) y(t) per k + uniformemente in I. Dimostrazione La parte complicata del teorema sta nel dimostrare che definitivamente per k k le soluzioni y k (t) possono essere definite in I e, volendo applicare il Teorema 9, nel verificare che le costanti M, d, L possono essere scelte in maniera uniforme (per esempio ciò accade se le traiettorie delle y k sono definitivamente contenute in un intorno compatto della traiettoria di y). Una volta provato ciò il risultato discende banalmente da (10) essendo (11) y(t) y k (t) [ y 0 y k + M t k + d f f k ] e L t, per t I, e per k + si ottiene la tesi. approfondimenti in coda al capitolo. Per i dettagli si vedano gli Esistono generalizzazioni di questi teoremi al caso di campi vettoriali non necessariamente lipschitziani, una delle quali è presentata nel seguito. Teorema 11 (di Kamke, di dipendenza continua dai dati (IV)) Siano date f, f k : Ω R R n R n continue, k = 1, 2,..., e punti (t k, y k ) Ω per k N. Supponiamo che il problema di Cauchy y = f(t, y) y( ) = y 0, abbia un unica soluzione y(t) nell intervallo chiuso e limitato I. Se (t k, y k ) (, y 0 ) e f k f per k + uniformemente sui compatti di Ω, detta y k (t)
10 10 DIPENDENZA DAI DATI INIZIALI una qualsiasi soluzione del problema di Cauchy y = f k (t, y) y(t k ) = y k, allora, definitivamente per k k, la funzione y k (t) può essere definita in I e si ha y k (t) y(t) per k + uniformemente su I. Dimostrazione Omessa. Approfondimenti Il Teorema di Peano, sui compatti Il seguente teorema asserisce che l ampiezza dell intervallo di esistenza di una soluzione può essere presa uniforme se il dato iniziale varia in un compatto. Teorema 12 (di Peano, sui compatti) Sia Ω R R n aperto e sia f : Ω R n continua. Fissato K Ω esiste ε = ε K > 0, dipendente solo da K, tale che per ogni (, y 0 ) K ogni soluzione massimale y(t) del problema di Cauchy y = f(t, y) y( ) = y 0 è definita almeno sull intervallo [ ε, + ε]. Dimostrazione Fissato un compatto K Ω, si possono trovare α, R > 0 tali che (12) C α,r (K) := (t,y) K C α,r (t, y) sia un compatto contenuto in Ω (verificarlo per esercizio). Posto M K = max f(s, z) : (s, z) C α,r (K)} sia infine ε K := minα, R/M K }. Preso un qualsiasi (, y 0 ) K, per costruzione si ha C α,r (, y 0 ) C α,r (K) Ω, da cui M := max f(s, z) : (s, z) C α,r (, y 0 )} M K e anche ε := α, R/M} ε K. Il Teorema di Peano e il Lemma 3.19 delle dispense garantiscono che ogni soluzione massimale del problema di Cauchy y = f(t, y), y( ) = y 0 sia definita almeno in I ε ( ) e a maggior ragione in I εk ( ).
11 APPROFONDIMENTI 11 Dimostrazione del Teorema 5 di dipendenza continua dai dati (III) L idea della dimostrazione è la seguente: si proverà che per t k, y k, f k sufficientemente vicini a, y 0, f, vale la disuguaglianza (11) in un intorno di, da cui seguirà che, ristrette a tale intorno, le traiettorie delle y k sono contenute in un intorno compatto della traiettoria di y. Inoltre, dimostreremo che se le traiettorie delle y k sono contenute in un intorno compatto della traiettoria di y fino al tempo t, allora vale (11) in un intorno di t. Ciò permetterà di concludere che (11) vale per ogni t I e che le traiettorie delle y k ristrette a t sono contenute in un intorno compatto della traiettoria di y (sembra un ragionamento circolare, ma non lo è!). Posto I = [a, b], poniamo per brevità ρ = b a e, come nella dimostrazione del Teorema di Peano sui compatti, prendiamo α, R > 0 tali che K 1 := C α,r (K) sia contenuto in Ω, dove K = T y è la traiettoria di y in I. Definiamo M := max f(s, x), M k := max f k (s, x), k = 1, 2,... (s,x) K 1 (s,x) K 1 Per ipotesi f k f uniformemente in K 1, quindi esiste k tale che definitivamente per k k si ha M k max f(s, x) + max f k (s, x) f(s, x) (M + 1). (s,x) K 1 (s,x) K 1 Preso δ = minα, R/(M + 1)} si ha che tutte le soluzioni di y = f k (t, y) con dati iniziali (t k, y k ) C α/2,r/2 (K) sono definite almeno in un intorno di t k di ampiezza δ/2. Essendo t k, y k y 0, eventualmente aumentando k possiamo assumere che t k δ/2 (in modo tale che y k (t) sia definita in ), y k y 0 R/2 e anche (13) [ yk y 0 + (M + 1) t k + ρ f k f ] e Lρ R. Dimostriamo che per ogni k k la funzione y k è definita in I e ivi soddisfa y k (t) y(t) R. Questa è essenzialmente una stima a priori: se è vera allora (t, y k (t)) K 1 per ogni t e si può utilizzare (10) per ottenere (14) y k (t) y(t) [ y k y 0 + M k t k + ρ f k f ] e L t [ y k y 0 + (M + 1) t k + ρ f k f ] e L t. Il secondo membro si maggiora con (13) da cui y k (t) y(t) R. In un certo senso si è dimostrato che finché y k (t) y(t) R è vera allora... y k (t)
12 12 DIPENDENZA DAI DATI INIZIALI y(t) R è vera (e di conseguenza vale (14))! Siccome è vera in allora è sempre vera. Vediamo ora i dettagli che dimostrano la validità di questo ragionamento, apparentemente circolare. Per k k si ha C δ/2,r/2 (t k, y k ) C δ,r (, y 0 ) K 1. Poiché per il Lemma 2.8 delle dispense le traiettorie di y k (t) non possono uscire da un cilindro di sicurezza centrato in (t k, y k ) allora sono contenute in K 1 almeno per t t k δ/2, perciò vale la disuguaglianza (14) per t =. Se ora tale disuguaglianza vale per ogni t [, τ] con τ < b allora per (14) e (13) si ha y k (τ) y(τ) < R, essendo τ < ρ. Il punto (τ, y k (τ)) è allora contenuto all interno del compatto K 1 ed è quindi possibile costruire un cilindro di sicurezza con centro tale punto e ancora contenuto in K 1. Ne consegue che y k (t) è definita almeno in un intorno (destro) di τ con traiettoria contenuta in K 1. Si può quindi estendere il ragionamento per concludere che (14) vale anche in un intorno di τ. In maniera analoga si ragiona per a < τ. In definitiva, detto I(, τ) l intervallo di estremi e τ, e posto J k := τ I : y k è definita in I(, τ) e vale (14) t I(, τ) } si è dimostrato che J k è un sottoinsieme chiuso (banale), aperto e non vuoto di I, dunque per connessione J k = I. Infine da (14)-(13) segue che max y k(t) y(t) [ ] y k y 0 + (M + 1) t k + ρ f k f e Lρ t I per ogni k k, e passando al limite per k + si ha la tesi.
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Matematica generale CTF
 Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
NOME:... MATRICOLA:... Scienza dei Media e della Comunicazione, A.A. 2007/2008 Analisi Matematica 1, Esame scritto del 08.02.2008. x 1.
 NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
analisi di sistemi retroazionati (2)
 : analisi di sistemi retroazionati (2) Marco Lovera Dipartimento di Elettronica e Informazione Politecnico di Milano lovera@elet.polimi.it Indice Piccolo guadagno Stabilita ingresso-uscita Guadagno L 2
: analisi di sistemi retroazionati (2) Marco Lovera Dipartimento di Elettronica e Informazione Politecnico di Milano lovera@elet.polimi.it Indice Piccolo guadagno Stabilita ingresso-uscita Guadagno L 2
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
FUNZIONI CONVESSE. + e x 0
 FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
La curva grafico della funzione, partendo dal punto A(a,f(a)), si snoda con continuità, senza interruzioni, fino ad approdare nel punto B(b,f(b)).
 Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Studio di una funzione ad una variabile
 Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
7 - Esercitazione sulle derivate
 7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Metodi numerici per la risoluzione di equazioni. Equazioni differenziali ordinarie
 Metodi numerici per la risoluzione di equazioni differenziali ordinarie Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ Lezione 5-31 ottobre 2005 Outline 1 Il problema di Cauchy Il problema
Metodi numerici per la risoluzione di equazioni differenziali ordinarie Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ Lezione 5-31 ottobre 2005 Outline 1 Il problema di Cauchy Il problema
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
0 ) = lim. derivata destra di f in x 0. Analogamente, diremo che la funzione f è derivabile da sinistra in x 0 se esiste finito il limite
 Questo breve file è dedicato alle questioni di derivabilità di funzioni reali di variabile reale. Particolare attenzione viene posta alla classificazione dei punti di non derivabilità delle funzioni definite
Questo breve file è dedicato alle questioni di derivabilità di funzioni reali di variabile reale. Particolare attenzione viene posta alla classificazione dei punti di non derivabilità delle funzioni definite
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Funzioni periodiche. Una funzione si dice periodica di periodo T se T > 0 è il più piccolo numero reale positivo tale che
 Funzioni periodiche Una funzione si dice periodica di periodo T se T > 0 è il più piccolo numero reale positivo tale che -T T In ogni intervallo di ampiezza pari a T il grafico di tale funzione si ripete.
Funzioni periodiche Una funzione si dice periodica di periodo T se T > 0 è il più piccolo numero reale positivo tale che -T T In ogni intervallo di ampiezza pari a T il grafico di tale funzione si ripete.
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
LA FUNZIONE INTEGRALE
 LA FUNZIONE INTEGRALE MAGLIOCURIOSO & CAMILLO magliocurioso@hotmail.it Sommario. In questa breve dispensa ho semplicementrascritto in L A TEX il contenuto di questa discussione: http://www.matematicamente.it/forum/
LA FUNZIONE INTEGRALE MAGLIOCURIOSO & CAMILLO magliocurioso@hotmail.it Sommario. In questa breve dispensa ho semplicementrascritto in L A TEX il contenuto di questa discussione: http://www.matematicamente.it/forum/
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
LEZIONE 16. Proposizione 16.1.2. Siano V e W spazi vettoriali su k = R, C. Se f: V W
 LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
Teoria dei Giochi. Anna Torre
 Teoria dei Giochi Anna Torre Almo Collegio Borromeo 26 marzo 2015 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2015.html COOPERAZIONE Esempio: strategie correlate e problema
Teoria dei Giochi Anna Torre Almo Collegio Borromeo 26 marzo 2015 email: anna.torre@unipv.it sito web del corso:www-dimat.unipv.it/atorre/borromeo2015.html COOPERAZIONE Esempio: strategie correlate e problema
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli. 03 - Equazioni differenziali lineari omogenee a coefficienti costanti.
 Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Introduzione Ordini parziali e Reticoli Punti fissi
 Introduzione Ordini parziali e Reticoli Punti fissi By Giulia Costantini (819048) & Giuseppe Maggiore (819050) Table of Contents ORDINE PARZIALE... 3 Insieme parzialmente ordinato... 3 Diagramma di Hasse...
Introduzione Ordini parziali e Reticoli Punti fissi By Giulia Costantini (819048) & Giuseppe Maggiore (819050) Table of Contents ORDINE PARZIALE... 3 Insieme parzialmente ordinato... 3 Diagramma di Hasse...
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Osservazioni sulla continuità per le funzioni reali di variabile reale
 Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici. a Corrente Alternata. Sergio Benenti 7 settembre 2013
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
DOMINI A FATTORIZZAZIONE UNICA
 DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
Capitolo 5. Funzioni. Grafici.
 Capitolo 5 Funzioni. Grafici. Definizione: Una funzione f di una variabile reale,, è una corrispondenza che associa ad ogni numero reale appartenente ad un insieme D f R un unico numero reale, y R, denotato
Capitolo 5 Funzioni. Grafici. Definizione: Una funzione f di una variabile reale,, è una corrispondenza che associa ad ogni numero reale appartenente ad un insieme D f R un unico numero reale, y R, denotato
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Funzioni di più variabili
 Funzioni di più variabili Introduzione Funzioni reali di più variabili reali Una unzione reale di due variabili è una unzione : D R dove il dominio D è un sottoinsieme di R. ESEMPI: - / ln. Considerazioni
Funzioni di più variabili Introduzione Funzioni reali di più variabili reali Una unzione reale di due variabili è una unzione : D R dove il dominio D è un sottoinsieme di R. ESEMPI: - / ln. Considerazioni
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
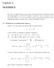 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMICA
 FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMICA DEFINIZIONE: Dato un numero reale a che sia a > 0 e a si definisce funzione esponenziale f(x) = a x la relazione che ad ogni valore di x associa uno e un solo
FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMICA DEFINIZIONE: Dato un numero reale a che sia a > 0 e a si definisce funzione esponenziale f(x) = a x la relazione che ad ogni valore di x associa uno e un solo
CURVE DI LIVELLO. Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello.
 CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
La funzione è continua nel suo dominio perchè y = f(x) è composizione di funzioni continue. Il punto x = 0 è un punto isolato per D f.
 FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
CAPITOLO 3 FONDAMENTI DI ANALISI DELLA STABILITA' DI SISTEMI NON LINEARI
 31 CAPITOLO 3 FONDAMENTI DI ANALISI DELLA STABILITA' DI SISTEMI NON LINEARI INTRODUZIONE L'obbiettivo di questo capitolo è quello di presentare in modo sintetico ma completo, la teoria della stabilità
31 CAPITOLO 3 FONDAMENTI DI ANALISI DELLA STABILITA' DI SISTEMI NON LINEARI INTRODUZIONE L'obbiettivo di questo capitolo è quello di presentare in modo sintetico ma completo, la teoria della stabilità
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
