Esercizi di Ricerca Operativa I
|
|
|
- Lucrezia Santi
- 8 anni fa
- Visualizzazioni
Transcript
1 Esercizi di Ricerca Operativa I Dario Bauso, Raffaele Pesenti May 10, 2006 Domande Programmazione lineare intera 1. Gli algoritmi per la programmazione lineare continua possono essere usati per la soluzione dei problemi di programmazione lineare binaria? 2. Quando la formulazione di un problema di programmazione lineare intera si dice migliore di un altra e perché? 3. Dimostrare che per ogni problema di programmazione lineare intera, con variabili vincolate superiormente, esiste una formulazione equivalente con solo variabili binarie. 4. Dato il seguente problema di programmazione lineare intera trasformarlo in problema di programmazione lineare binaria. max z = +40x a + 42x b 2x a + x b 6 7x a + 3x b 15 0 x a 4 0 x b Dimostrare che le seguenti condizioni booleane su variabili binarie possono essere espresse con vincoli lineari: 1) x 3 = x 1 OR x 2, 2) x 3 = x 1 AND x 2, 3) x 3 = NOT x Perché è estremamente importante sapere risolvere problemi di programmazione lineare binaria? 7. Cosa è un metodo di enumerazione implicita per la soluzione di un problema di programmazione lineare binaria? 8. Quale è l idea alla base del Branch & Bound? 9. L algoritmo del Branch & Bound determina sempre la soluzione ottima di un problema di programmazione lineare binaria con un numero finito di variabili in un tempo finito? 1
2 10. Quale è il numero massimo dei nodi dell albero di ricerca generato da un algoritmo di Branch & Bound applicato ad un problema di programmazione lineare binaria con n variabili? 11. Quale è la profondità massima dell albero di ricerca generato da un algoritmo di Branch & Bound applicato ad un problema di programmazione lineare binaria con n variabili? 12. Stimare quale è il tempo di esecuzione massimo che l algoritmo di Branch & Bound può richiedere per risolvere un problema con n = 1000 variabili binarie. Supporre di avere a disposizione un calcolatore da 10 teraflop e che il calcolatore sia capace di eseguire risolvere i problemi rilassati ad ogni nodo in sole 100 operazioni floating point. Approssimare per semplicità 2 10 con Stimare quale è il numero massimo di nodi che l algoritmo di Branch & Bound può riuscire ad esplorare in secondi (circa 2:45 ore). Indicare la dimensione massima, in termini di numero di variabili, dell istanza di programmazione lineare binaria che può essere risolta in tale tempo nel caso in cui si il Branch & Bound debba generare un albero di ricerca completo. Supporre di avere a disposizione un calcolatore da 10 teraflop e che il calcolatore sia capace di eseguire risolvere i problemi rilassati ad ogni nodo in sole 100 operazioni floating point. Approssimare per semplicità 2 10 con Come mai, a volte, il Branch & Bound riesce a risolvere problemi di dimensioni significative in tempi ragionevoli? 15. Perché in molti software commerciali l algoritmo del Branch & Bound si interrompe quando ha trovato una soluzione che è sicuramente entro il 5% (o l 1%) dall ottimo? 16. Cosa è un metodo euristico di soluzione di un problema di programmazione lineare binaria? 17. Come ci si comporta se non si riesce a trovare la soluzione esatta di un problema di programmazione lineare intera in tempi ragionevoli, ad esempio attraverso un algoritmo di Branch & Bound? 18. Dato un algoritmo di Branch & Bound, cosa vuol dire che l esplorazione dell albero di ricerca avviene in modo depth first / best bound first? 19. Dato un algoritmo di Branch & Bound, quali sono i vantaggi e gli svantaggi legati alla visita dell albero di ricerca in modo depth first / best bound first? (Dare per scontato che si sappia già cosa significa depth first / best bound first.) 20. Quale tra il depth first e il best bound first è utilizzato nella pratica dai software commerciali? 21. Dato un problema di programmazione binaria, in che ordine vengono scelte le variabili che vengono progressivamente vincolate a valori interi nelle successive iterazioni del Branch & Bound? 22. Dato un problema di programmazione lineare binaria, cosa di intende per problema rilassato? 23. Quale è l utilità di risolvere un problema rilassato invece che il programmazione lineare binaria originale? 24. Quali sono i rilassamenti più utilizzati nella pratica per i problemi di programmazione lineare binaria? 2
3 25. Cosa si intende per rilassamento continuo / per eliminazione / surrogato / lagrangiano? 26. Sia dato un problema di massimo di programmazione lineare intera. Quando un rilassamento può dirsi migliore di un altro? Esiste un rilassamento ottimo per la classe dei rilassamenti lagrangiani? E per la classe dei rilassamenti surrogati? 27. Quali relazioni di dominanza esistono tra i seguenti rilassamenti continuo / per eliminazione / surrogato / lagrangiano. Perché non si usa uno solo di essi? 28. Sia dato un problema di programmazione lineare binaria in cui bisogna MINIMIZZARE una data funzione obiettivo. Si risolvono tre rilassamenti diversi. Il rilassamento R 1 dà come soluzione z R1 = 150, il rilassamento R 2 dà come soluzione z R2 = 140, il rilassamento R 3 dà come soluzione z R3 = 120. Quale dei tre rilassamenti si deve considerare migliore per l istanza data? 29. Sia dato il seguente problema di programmazione lineare binaria max z = +40x x x x x 5 +42x x x x x x x x x x 5 36 x 1, x 2, x 3, x 4, x 5 {0, 1}. Il suo rilassamento surrogato, in cui il primo vincolo è pesato 2 e il secondo 3, dà luogo alla soluzione x RS = (0, 0, 1, 0, 1) con z RS = 89. Indicare qualitativamente come si dovrebbero cambiare i valori dei pesi per sperare di ottenere un rilassamento surrogato migliore. 30. Dato il seguente problema di programmazione lineare binaria, sapendo che la soluzione ottima del suo rilassamento per eliminazione del primo vincolo è x RE = (0, 1, 1, 0, 1), valutare una stima dell errore percentuale che si compie accettando la soluzione ˆx = (1, 1, 1, 0, 0) piuttosto che cercare la soluzione ottima. max z = +43x x x x x 5 +40x x x x x x x 2 5x x x 5 33 x 1, x 2, x 3, x 4, x 5 {0, 1}. 31. Dato un problema di programmazione lineare intera come può essere provata l ottimalità di una soluzione? E la sua ammissibilità? 32. Cosa vuol dire che un problema è difficile e perchè è importante la Programmazione Lineare Intera nell ambito di tali problemi. 33. Cosè un problema di PLI? 34. In quali casi bisogna ricorrere alle variabili intere? 35. Si definisca un problema di Ottimizzazione combinatoria. 3
4 36. Si definisca a parole il problema dello zaino (istanza, soluzione e obiettivo). 37. Si scriva il modello del problema dello zaino. 38. Citare e descrivere un esempio di applicazione del problema dello zaino. 39. Si definisca a parole il problema del bin packing (istanza, soluzione e obiettivo). 40. Si scriva il modello del problema del bin packing. 41. Citare e descrivere un esempio di applicazione del problema del bin packing. 42. Si definisca a parole il problema dello scheduling (istanza, soluzione e obiettivo). 43. Si scriva il modello del problema di scheduling. 44. Si definisca a parole il problema del mix di produzione con costi di set-up (istanza, soluzione e obiettivo). 45. Si scriva il modello del problema del mix di produzione con costi di set-up. 46. Si definisca a parole il problema del commesso viaggiatore (istanza, soluzione e obiettivo). 47. Si scriva il modello del problema del commesso viaggiatore. 48. Si definisca una soluzione di tipo covering. 49. Si definisca una soluzione di tipo packing. 50. Si definisca una soluzione di tipo partitioning. 51. Si definisca un problema di covering. 52. Si definisca un problema di packing. 53. Si definisca un problema di partitioning. 54. Si definisca la matrice e il vettore di incidenza e i vincoli di covering, packing e partitioning. Risposte agli esercizi Notazione Nelle risposte successive max{z = cx : Ax b, x {0, 1}} indica il generico problema binario max z = cx Ax b x {0, 1} x indica la soluzione ottima del problema binario, e z = cx il valore assunto all ottimo dalla funzione obiettivo. x RC indica la soluzione ottima del rilassamento continuo di un problema binario, e zrc = cx RC il valore assunto all ottimo dalla funzione obiettivo del rilassamento continuo. 4
5 Risposte (1) Affinché un problema di programmazione binaria max{z = cx : Ax b, x {0, 1}} possa essere dato in input a un algoritmo per la programmazione lineare continua bisogna rilassare in vincoli di interezza e considerare il problema max{z RC = cx : Ax b, 0 x 1}. In generale la soluzione ottima x RC del problema rilassato risulta essere frazionaria. Vale inoltre la relazione cx cx RC. dove x è la soluzione ottima del problema binario. È infatti banale osservare che x è ammissibile per il problema rilassato e quindi che il valore ottimo del problema rilassato non può che essere migliore o al più uguale a quello ottimo del problema intero. Gli algoritmi per la programmazione lineare continua possono essere utilizzati per determinare l ottimo di un problema di programmazione intera nel caso in cui i vincoli del rilassamento continuo definiscono un poliedro che abbia come vertice ottimo una soluzione intera. Questa possibilità è sfruttata dagli algoritmi di soluzione in due modi differenti. 1) I metodi basati sui piani di taglio aggiungono successivamente vincoli al rilassamento continuo del problema originale in modo da eliminare progressivamente le soluzioni ottime ma frazionarie. Tali metodi iterano il loro procedimento fino a ottenere formulazioni che definiscono poliedri le con soluzioni ottime intere. 2) Il Branch & Bound suddivide ricorsivamente le soluzioni in sottopoliedri fino a quando tali sottopoliedri hanno vertici ottimi interi oppure certamente non contengono la soluzione ottima. (2) Una formulazione di un problema di programmazione lineare intera max{z = cx : Ax b, x {0, 1}} si dice migliore della formulazione max{z = cx : Âx ˆb, x {0, 1}} se le soluzioni ammissibili intere delle due formulazioni sono le stesse ma il poliedro P = {x : Ax b, 0 x 1} associato alla alla prima formulazione è incluso nel poliedro ˆP = {x : Âx ˆb, 0 x 1} associato alla seconda formulazione. In tale situazione è vero che cx cx RC cˆx RC cx. per qualunque funzione di costo Quindi, qualunque sia la funzione obiettivo, la soluzione del rilassamento continuo della prima formulazione fornisce una stima migliore del valore ottimo del problema di programmazione lineare intera rispetto al rilassamento continuo della seconda formulazione. (3) Sia dato un problema intero la cui generica variabile x i N è limitata superiormente dal vincolo 0 x i u i, dove u i è una costante. Per ottenere il corrispondente problema binario basta sostituire nel problema originale la variabile x i con la seguente combinazione di variabili binarie log 2 u i k=0 2 k y ki = y 0i +2y 1i +4y 2i log 2 ui y log2 u i,i. I valori assunti da ogni vettore di variabili (y 0i, y 1i, y 2i,..., y log2 u i,i) corrisponde all espressione in codice binario del valore della variabile x i. (4) Si pone x a = y 0a + 2y 1a + 4y 2a e x b = y 0b + 2y 1b ottenendo max z = +40(y 0a + 2y 1a + 4y 2a ) + 42(y 0b + 2y 1b ) 2(y 0a + 2y 1a + 4y 2a ) + (y 0b + 2y 1b ) 6 7(y 0a + 2y 1a + 4y 2a ) + 3(y 0b + 2y 1b ) 15 0 y 0a + 2y 1a + 4y 2a 4 5
6 0 y 0b + 2y 1b 3, da cui max z = +40y 0a + 80y 1a + 160y 2a + 42y 0b + 84y 1b 2y 0a + 4y 1a + 16y 2a + y 0b + 2y 1b 6 7y 0a + 14y 1a + 28y 2a + 3y 0b + 6y 1b 15 0 y 0a + 2y 1a + 4y 2a 4 0 y 0b + 2y 1b 3. x 3 x 1 + x 2 (5) 1) La condizione x 3 = x 1 OR x 2 può essere espressa dall insieme delle seguenti condizioni x 3 x 1 x 3 x 2 x 3 x 1 + x 2 1 2) La condizione x 3 = x 1 AND x 2 può essere espressa dall insieme delle seguenti condizioni x 3 x 1 x 3 x 2 3) La condizione x 3 = NOT x 2 può essere espressa come x 3 = 1 x 2. (6) È estremamente importante sapere risolvere problemi di programmazione lineare binaria perché, ad esempio, tramite di essi si possono modellare tutte quelle situazioni decisionali descrivibili attraverso la logica del primo ordine. Più tecnicamente si possono risolvere tutti i problemi della classe NP. (Gli interessati possono vedere le dispense corso di Ricerca Operativa II sulla complessità computazionale.) (7) Un metodo è detto di enumerazione implicita se determina la soluzione ottima di un problema esplorando in modo esplicito o implicito tutte le soluzioni del problema stesso. In particolare si definisce esplorazione esplicita di una soluzione ˆx il calcolo del corrispondente valore cˆx. Viceversa si definisce esplorazione implicita di una classe di soluzioni l escludere a priori che a tutti, o ad almeno alcuni, elementi della classe sia associato il valore ottimo di cx senza la necessità di enumerare esplicitamente le soluzioni considerate. (8) Il Branch & Bound è un metodo di enumerazione implicita delle soluzioni. Il Branch & Bound suddivide ricorsivamente l insieme delle soluzioni di un problema in sottoinsiemi. La suddivisione si ferma a quando per ognuno dei sottoinsiemi si riesce a valutare il valore cx della migliore soluzione inclusa nel sottoinsieme oppure si può escludere che il sottoinsieme contenga la soluzione ottima. I sottoinsiemi generati possono essere organizzati ad albero. Ogni sottoinsieme generato corrisponde ad un nodo dell albero. Ad ogni iterazione il Branch & Bound analizza il sottoinsieme di soluzioni associato ad un nodo dell albero di ricerca e determina una stima ẑ del valore cx della migliore soluzione del sottoinsieme. Se ẑ non esiste perché tutte le soluzioni non sono ammissibili o ẑ risulta peggiore della migliore soluzione intera correntemente disponibile all algoritmo, il Branch & Bound esclude da ulteriore analisi le soluzioni del sottoinsieme considerato. In questo caso si dice che il Branch & Bound pota il nodo dell albero di ricerca. 6
7 (9) L algoritmo del Branch & Bound determina sempre la soluzione ottima di un problema di programmazione lineare binaria con un numero finito di variabili in un tempo finito. Infatti, per svolgere la ricerca dell ottimo, l algoritmo produce un albero con un numero finito di nodi e, in ogni nodo, risolve un problema di programmazione lineare continua in un tempo finito. (10) L albero di ricerca generato da un algoritmo di Branch & Bound applicato a un problema di programmazione lineare binaria con n variabili contiene al più 2 n+1 1 nodi. (11) La profondità massima dell albero di ricerca generato da un algoritmo di Branch & Bound applicato ad un problema di programmazione lineare binaria con n variabili è di n livelli. Ad ogni livello infatti è fissato il valore di una delle n variabili. (12) Nel caso peggiore l algoritmo di Branch & Bound deve esplorare tutti i 2 n+1 1 nodi dell albero di ricerca. Siccome in ogni nodo il Branch & Bound deve risolvere un problema rilassato si ottiene che nel caso peggiore devono essere eseguite ( ) = operazioni floating point. Un calcolatore da 10 teraflop, cioè da operazioni al secondo, impiegherebbe /10 13 = secondi. Per avere un termine di paragone si tenga presente che si suppone che l età dell universo sia di secondi. (13) Un calcolatore da 10 teraflop esegue operazioni al secondo. Se per risolvere un problema rilassato servono 100 operazioni, l algoritmo di Branch & Bound può esplorare nodi al secondo e quindi nodi in secondi. Un albero di ricerca associato ad un istanza di n variabili binarie contiene al più 2 n+1 1 nodi. Ponendo 2 n+1 1 = si ottiene n 50. (14) A volte il Branch & Bound riesce a risolvere problemi anche con numerose variabili in tempi ragionevoli in quanto riesce ad escludere a priori sottoinsiemi di soluzioni molto grandi. Le prestazioni dell algoritmo dipendono in maniera drammatica dal livello a cui avvengono le potature dei nodi dell albero di enumerazione. È fondamentale quindi che i problemi rilassati che vengono risolti ad ogni nodo: risultino quanto più spesso possibile inammissibili se il corrispondente problema intero non ammette soluzioni ammissibili oppure forniscano un bound sul valore ottimo il più vicino possibile a quello del problema intero. (15) I problemi di programmazione lineari interi o binari spesso presentano moltissime soluzioni ottime equivalenti. Molti software commerciali che implementano il Branch & Bound si interrompono quando hanno trovato una soluzione che è sicuramente entro il 5% (o l 1%) dall ottimo per proprio per evitare di enumerare tutte queste soluzioni. (16) I metodi euristici di soluzione sono algoritmi che risolvono i problemi di ottimizzazione. Essi utilizzano in genere regole di buon senso e restituiscono soluzioni ammissibili ma non necessariamente ottime. I metodo euristici forniscono quindi soluzioni peggiori dei metodi di enumerazione implicita che restituiscono soluzioni ottime. I metodi euristici però terminano tipicamente in un numero di passi molto inferiore a quelli degli algoritmi di enumerazione. 7
8 (17) Dato un problema programmazione lineare intera se non si riesce a trovare la soluzione ottima in tempi ragionevoli, ad esempio attraverso un algoritmo di Branch & Bound, si passa a qualche metodo euristico. In questo caso si sacrifica la qualità della soluzione in cambio di una risposta veloce. (18) Dato un algoritmo di Branch & Bound, si dice che l esplorazione dell albero di ricerca avviene in modo depth first se ad ogni iterazione l algoritmo sceglie di esplorare uno tra i nodi figli del nodo appena esplorato. Se il nodo appena esplorato è stato potato o non ha figli, l algoritmo passa al nodo di più basso livello non ancora esplorato. Si dice che l esplorazione dell albero di ricerca avviene in modo best bound first se ad ogni iterazione l algoritmo sceglie di esplorare uno tra i nodi a cui è associato il migliore bound della soluzione ottima. (19) Dato un algoritmo di Branch & Bound, i vantaggi del depth first sono legati al fatto che ad ogni iterazione devono essere memorizzati al più n nodi già esplorati e n nodi in attesa di essere esplorati. Gli svantaggi sono legati al fatto che ad ogni iterazione si può scegliere solo tra un numero molto limitato di nodi e quindi le soluzioni che si trovano all inizio dell esplorazione possono essere molto scadenti. I vantaggi del best bound first sono dovuti al fatto che la prima soluzione intera che si determina con questa strategia di ricerca o è ottima o, in generale, è molto vicina ad essere tale. Gli svantaggi è che il numero dei nodi che rimangono aperti ad ogni iterazione può crescere notevolmente e occupare tutto lo spazio di memoria disponibile. (20)I software commerciali tipicamente usano una strategia mista tra depth first e best bound first. Essi applicano una strategia depth first fino a quando i bound dei nodi figli dell ultimo nodo esplorato non risultano scadenti. Quando ciò accade, abbandonano il nodo corrente e ripartono con una strategia depth first dal nodo aperto con il migliore bound. (21) Quando è possibile è meglio scegliere prima le variabili più importanti, cioè quelle variabili in cui imporre un valore intero implica dei vincoli molto stringenti (possibilmente addirittura l interezza) sul maggior numero delle rimanenti variabili non ancora fissate. (22) Dato un problema di programmazione lineare binaria, si definisce rilassamento un problema tale che: 1) ha un insieme di soluzioni ammissibili che include le soluzioni del problema originale, 2) ha una funzione obiettivo il cui valore è sempre non peggiore di quello della funzione obiettivo del problema originale quando tali funzioni sono calcolate rispetto a soluzioni ammissibili per entrambe i problemi. Tipicamente un problema rilassato si ottiene rendendo più deboli alcuni dei vincoli del problema originale. Ad esempio nel rilassamento continuo si rinuncia all interezza delle variabili. (23) I problemi rilassati sono, in generale, più semplici da risolvere rispetto al problema originale. La soluzione ottima del problema rilassato permette di determinare una stima del valore ottimo del problema originale, anche se di norma tale soluzione non è ammissibile per il problema originale. (24) Il rilassamento lineare (o continuo) e il rilassamento lagrangiano. 8
9 (25) Dato un problema di programmazione binaria, nel rilassamento continuo viene a mancare il vincolo di interezza che viene sostituito dal vincolo 0 x i 1 per ogni variabile binaria nel problema originale. Nel rilassamento per eliminazione vengono eliminati alcuni dei vincoli (ma non quello di interezza). Nel rilassamento surrogato alcuni gruppi di vincoli vengono sostituiti da loro combinazioni coniche. Nel rilassamento lagrangiano alcuni dei vincoli vengono trasformati in componenti pesate dell obiettivo. (26) Un rilassamento può dirsi migliore di un altro quando fornisce una stima migliore del valore ottimo del problema originale. Nel caso di problemi di massimizzazione il valore ottimo di un problema rilassato z R è sempre maggiore del valore ottimo z del problema originale. Un rilassamento R è quindi migliore di un altro rilassamento ˆR se z ˆR z R z. Il valore di z R è infatti una migliore stima di z. Il valore del ottimo del rilassamento lagrangiano z RL dipende dai pesi che sono stati utilizzati per rilassare i vincoli. Il rilassamento lagrangiano surrogato ottimo è quindi quello per cui i pesi scelti rendono minimo il valore z RL. Il lagrangiano surrogato ottimo viene detto duale lagrangiano. Identico discorso vale per il rilassamento surrogato. (27) Il rilassamento surrogato ottimo è non peggiore del rilassamento lagrangiano ottimo che, a sua volta, è non peggiore sia del rilassamento lineare che di quello per eliminazione. Non esiste relazione di dominanza fra gli ultimi due rilassamenti. Non si usa solo un tipo di rilassamento perché alcuni di essi sono più facili da risolvere, altri danno stime migliori del valore ottimo del problema originale. (28) Trovandosi a risolvere un problema di minimizzazione vale che qualunque rilassamento assume un valore inferiore o uguale all ottimo e quindi z R3 z R2 z R1 z. Poiché z z R1 z z R2 z z R3, ne consegue che z R1 è una migliore stima di z, da cui R 1 deve considerarsi il migliore rilassamento per il caso in questione. (29) Dato max z = +40x x x x x 5 +42x x x x x x x x x x 5 36 x 1, x 2, x 3, x 4, x 5 {0, 1} Si osserva che la soluzione del rilassamento surrogato x RS = (0, 0, 1, 0, 1) soddisfa il primo vincolo ma non il secondo. Per sperare di ottenere un rilassamento surrogato migliore converrebbe provare ad aumentare il peso assegnato al secondo vincolo e diminuire il peso assegnato al primo vincolo. (30) Il valore della funzione obiettivo del rilassamento per eliminazione è z RE = 148. Il valore della funzione obiettivo associato alla soluzione ammissibile è ẑ = 137. L errore percentuale che si compie accettando ˆx è e% = z ẑ ẑ z RE ẑ ẑ = %. (31) In generale non si può provare l ottimalità di una soluzione di un problema di programmazione lineare binaria. Al più si può stimare per eccesso la sua distanza dall ottimo facendo uso dei risultati di 9
10 un rilassamento. Verificare l ammissibilità di una soluzione è invece banale, basta controllare che tale soluzione soddisfi tutti i vincoli del problema. (32) I problemi difficili sono quelli per i quali è molto improbabile che si trovino algoritmi polinomiali esatti di soluzione. La PLI rappresenta un problema di riferimento a cui possibilmente trasformare o ridurre ogni altro problema difficile (NP-hard). (33)È un problema di ottimizzazione in cui: La funzione obiettivo c è lineare le condizioni che descrivono l insieme delle soluzioni ammissibili sono lineari le soluzioni ammissibili sono intere i parametri sono deterministici (34) i) Per modellare leve decisionali intrinsecamente intere (macchine, persone...); ii) per esprimere relazioni logiche OR, IF...THEN tra le variabili; iii) per modellare scelte mutamente esclusive (vero/falso, appartenenza/non appartenenza) (35) Sono dati un insieme finito N = 1..., N e un vettore c T = [c 1,..., c n ]. Dato un generico sottoinsieme F N, si definisce c(f ) come c(f ) = i F c i. Sia data una collezione S di sottoinsiemi di N, allora un problema di ottimizzazione combinatoria è dato da max F S c(f ). (36) Istanza: un insieme finito U, dove ogni i U è caratterizzato da un volume s i N, da un valore v i N. Inoltre sia dato il volume dello zaino B N. Soluzione: un sottoinsieme U U tale che il volume occupato non ecceda il volume dello zaino, i.e., i U s i B. Obiettivo: il valore totale degli elementi scelti sia massimo, max U i U c i. (37) Il modello del problema dello zaino è il seguente n max c i x i i=1 n s i x i B i=1 x i = {0, 1}, i = 1..., n (38) Capital Budgeting. Obiettivo: max ritorno atteso; vincoli: non investire più capitale di quello a disposizione; leve decisionali: scelta degli investimenti: dati tecnologici: p i ritorno investimento imo, a i capitale richiesto investimento imo, b capitale disponibile. (39) Istanza: un insieme finito U, dove ogni u U è caratterizzato da un volume s u N, e dei contenitori di volume B N. Soluzione: una partizione di U in sottoinsiemi U(i), i = 1,..., n ognuno dei quali assegnato a un bin, e tale che il volume occupato in ogni bin i non sia maggiore di B, i.e., u U(i) s u B. Obiettivo: il numero totale di bin sia minimo. 10
11 (40) Il modello del problema del bin packing è il seguente min n i=1 y i n s j x ij By i j=1 n x ij = 1 i=1 x ij {0, 1}, i = 1,..., n j = 1,..., n i, j = 1,..., n (41) Schedulazione operazioni di ortopedia. Obiettivo: minimizzare numero di giorni utilizzati; vincoli: ogni operazione deve essere eseguita, la giornata lavorativa ima non deve durare più di B i ore; leve decisionali: quali giorni dedicare alle operazioni, quali operazioni effettuare in un dato giorno; dati tecnologici: a j durata operazione jma, B i tempo disponibile per operare il giorno imo. (42) Istanza: un unica macchina e un insieme finito di operazioni U, dove ogni operazione i U è caratterizzata da un tempo di esecuzione p i N e un tempo di rilascio r i N. Soluzione: una sequenziazione delle operazioni in modo che nessuna operazione sia venga iniziata prima del proprio tempo di rilascio, venga eseguita contemporaneamente a un altra. Obiettivo: il tempo medio di completamento delle operazioni sia minimo, i.e., min C i. (43) Il modello del problema di scheduling è il seguente (x ij = 1 se i precede j e 0 altrimenti) min n i=1 C i C i r i + p i C i C j + p i Mx ij x ij {0, 1}, i = 1,..., n i, j = 1,..., n, i j i, j = 1,..., n (44) Istanza: un insieme finito di tipologie di prodotti U e un insieme di risorse R, dove ogni unità di prodotto i U è caratterizzato da un profitto c i N, da un consumo a ji di risorsa j, e da un costo fisso di inizio produzione d i. Soluzione: un mix di produzione x che non richieda più risorse di quelle disponibili, i.e., n i=1 a jix i b j, j = 1,..., m, Obiettivo: il profitto del mix di produzione sia massimo al netto dei costi di set-up. (45) Il modello del problema del mix di produzione è il seguente max i U(c i x i d i y i ) a ji x i b j i U x i My i j R i U x i 0, y i = {0, 1}, i U. 11
12 (46) Istanza: una rete completa G(V, E) in cui a ogni arco e è associato un costo c e di attraversamento, un nodo origine s V. Soluzione: un circuito C={s,..., i,..., s}, che visiti tutti i nodi una sola volta, si richiuda sul nodo origine s e rispetti gilgli eventuali orientamenti degli archi. Obiettivo: il costo totale del circuito sia minimo, i.e., detto E(C) l insieme degli archi attraversati, min C:circuiti e E(C) c e. (47) modello del problema del commesso viaggiatore è il seguente e E(S) min c e x e e E x e = 2 i V e δ(i) x e S 1 S V x e {0, 1}, e E. (48) Siano dati un insieme finito M = {1,..., m}, un insieme S = {F 1,..., F n } dei sottoinsiemi di M e un insieme F = {F 1,..., F r } di sottoinsiemi di M tali che F S. L insieme F si dice covering se i F i = M. (49) Siano dati un insieme finito M = {1,..., m}, un insieme S = {F 1,..., F n } dei sottoinsiemi di M e un insieme F = {F 1,..., F r } di sottoinsiemi di M tali che F S. L insieme F si dice packing se F i F j = for all F i, F j F. (50) Siano dati un insieme finito M = {1,..., m}, un insieme S = {F 1,..., F n } dei sottoinsiemi di M e un insieme F = {F 1,..., F r } di sottoinsiemi di M tali che F S. L insieme F si dice partitioning se i F i = M e F i F j = for all F i, F j F. (51) Istanza: dati un insieme finito M = {1,..., m} e una funzione c : S N che assegni un costo a ogni sottoinsieme F i di M. Soluzione: un covering F = {F 1,..., F r }. Obiettivo: il costo del covering sia minimo, i.e., min F S F i F c(f i). (52) Istanza: dati un insieme finito M = {1,..., m} e una funzione c : S N che assegni un costo a ogni sottoinsieme F i di M. Soluzione: un packing F = {F 1,..., F r }. Obiettivo: il costo del packing sia massimo, i.e., max F S F i F c(f i). (53) Istanza: dati un insieme finito M = {1,..., m} e una funzione c : S N che assegni un costo a ogni sottoinsieme F i di M. Soluzione: un partitioning F = {F 1,..., F r }. Obiettivo: il costo del partitioning sia minimo, i.e., min F S F i F c(f i). (54) Matrice di incidenza A R m n (una riga per ogni elemento di M e una colonna per ogni elemento F j di S): 1 se i F j a ij = 0 altrimenti 12
13 Vettore di incidenza x R n 1 (una riga per ogni elemento F j di S): 1 se viene scelto F i x i = 0 altrimenti Covering: Ax 1; Packing: Ax 1; Partitioning: Ax = 1. 13
Il Metodo Branch and Bound
 Il Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 4 Novembre 2014 Ricerca Operativa 2 Laurea Magistrale in Ingegneria Gestionale
Il Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 4 Novembre 2014 Ricerca Operativa 2 Laurea Magistrale in Ingegneria Gestionale
Ottimizzazione Multi Obiettivo
 Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
Seconda Prova di Ricerca Operativa. Cognome Nome Numero Matricola A 1/12 A 2/12
 A / A / Seconda Prova di Ricerca Operativa Cognome Nome Numero Matricola Nota: LA RISOLUZIONE CORRETTA DEGLI ESERCIZI CONTRADDISTINTI DA UN ASTERISCO È CONDIZIONE NECESSARIA PER IL RAGGIUNGIMENTO DELLA
A / A / Seconda Prova di Ricerca Operativa Cognome Nome Numero Matricola Nota: LA RISOLUZIONE CORRETTA DEGLI ESERCIZI CONTRADDISTINTI DA UN ASTERISCO È CONDIZIONE NECESSARIA PER IL RAGGIUNGIMENTO DELLA
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
Capitolo 5: Ottimizzazione Discreta. E. Amaldi DEI, Politecnico di Milano
 Capitolo 5: Ottimizzazione Discreta E. Amaldi DEI, Politecnico di Milano 5.1 Modelli di PLI, formulazioni equivalenti ed ideali Il modello matematico di un problema di Ottimizzazione Discreta è molto spesso
Capitolo 5: Ottimizzazione Discreta E. Amaldi DEI, Politecnico di Milano 5.1 Modelli di PLI, formulazioni equivalenti ed ideali Il modello matematico di un problema di Ottimizzazione Discreta è molto spesso
Metodi e Modelli per l Ottimizzazione Combinatoria Il problema del flusso di costo minimo
 Metodi e Modelli per l Ottimizzazione Combinatoria Il problema del flusso di costo minimo L. De Giovanni G. Zambelli 1 Problema del flusso a costo minimo Il problema del flusso a costo minimo é definito
Metodi e Modelli per l Ottimizzazione Combinatoria Il problema del flusso di costo minimo L. De Giovanni G. Zambelli 1 Problema del flusso a costo minimo Il problema del flusso a costo minimo é definito
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
1) Descrivere dettagliatamente a quale problema di scheduling corrisponde il problema.
 Un veicolo viene utilizzato da una società di trasporti per trasportare beni a partire da un unico deposito verso prefissate località di destinazione. Si supponga che occorre trasportare singolarmente
Un veicolo viene utilizzato da una società di trasporti per trasportare beni a partire da un unico deposito verso prefissate località di destinazione. Si supponga che occorre trasportare singolarmente
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Ricerca Operativa Esercizi sul metodo del simplesso. Luigi De Giovanni, Laura Brentegani
 Ricerca Operativa Esercizi sul metodo del simplesso Luigi De Giovanni, Laura Brentegani 1 1) Risolvere il seguente problema di programmazione lineare. ma + + 3 s.t. 2 + + 2 + 2 + 3 5 2 + 2 + 6,, 0 Soluzione.
Ricerca Operativa Esercizi sul metodo del simplesso Luigi De Giovanni, Laura Brentegani 1 1) Risolvere il seguente problema di programmazione lineare. ma + + 3 s.t. 2 + + 2 + 2 + 3 5 2 + 2 + 6,, 0 Soluzione.
Corso di Matematica per la Chimica
 Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
Un modello matematico di investimento ottimale
 Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
e-dva - eni-depth Velocity Analysis
 Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
Ricerca Operativa Branch-and-Bound per problemi di Programmazione Lineare Intera
 Ricerca Operativa Branch-and-Bound per problemi di Programmazione Lineare Intera L. De Giovanni AVVERTENZA: le note presentate di seguito non hanno alcuna pretesa di completezza, né hanno lo scopo di sostituirsi
Ricerca Operativa Branch-and-Bound per problemi di Programmazione Lineare Intera L. De Giovanni AVVERTENZA: le note presentate di seguito non hanno alcuna pretesa di completezza, né hanno lo scopo di sostituirsi
Correttezza. Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1. Dispensa 10. A. Miola Novembre 2007
 Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 10 Correttezza A. Miola Novembre 2007 http://www.dia.uniroma3.it/~java/fondinf1/ Correttezza 1 Contenuti Introduzione alla correttezza
Corso di Laurea Ingegneria Informatica Fondamenti di Informatica 1 Dispensa 10 Correttezza A. Miola Novembre 2007 http://www.dia.uniroma3.it/~java/fondinf1/ Correttezza 1 Contenuti Introduzione alla correttezza
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Sistemi Operativi mod. B. Sistemi Operativi mod. B A B C A B C P 1 2 0 0 P 1 1 2 2 3 3 2 P 2 3 0 2 P 2 6 0 0 P 3 2 1 1 P 3 0 1 1 < P 1, >
 Algoritmo del banchiere Permette di gestire istanze multiple di una risorsa (a differenza dell algoritmo con grafo di allocazione risorse). Ciascun processo deve dichiarare a priori il massimo impiego
Algoritmo del banchiere Permette di gestire istanze multiple di una risorsa (a differenza dell algoritmo con grafo di allocazione risorse). Ciascun processo deve dichiarare a priori il massimo impiego
ESEMPIO P.L. : PIANIFICAZIONE DI INVESTIMENTI
 ESEMPIO P.L. : PIANIFICAZIONE DI INVESTIMENTI PROBLEMA: un azienda deve scegliere fra due possibili investimenti al fine di massimizzare il profitto netto nel rispetto delle condizioni interne e di mercato
ESEMPIO P.L. : PIANIFICAZIONE DI INVESTIMENTI PROBLEMA: un azienda deve scegliere fra due possibili investimenti al fine di massimizzare il profitto netto nel rispetto delle condizioni interne e di mercato
Modelli di Programmazione Lineare. PRTLC - Modelli
 Modelli di Programmazione Lineare PRTLC - Modelli Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Come ricavare una stima dell ottimo Rilassamento continuo - generazione
Modelli di Programmazione Lineare PRTLC - Modelli Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver commerciali Come ricavare una stima dell ottimo Rilassamento continuo - generazione
VC-dimension: Esempio
 VC-dimension: Esempio Quale è la VC-dimension di. y b = 0 f() = 1 f() = 1 iperpiano 20? VC-dimension: Esempio Quale è la VC-dimension di? banale. Vediamo cosa succede con 2 punti: 21 VC-dimension: Esempio
VC-dimension: Esempio Quale è la VC-dimension di. y b = 0 f() = 1 f() = 1 iperpiano 20? VC-dimension: Esempio Quale è la VC-dimension di? banale. Vediamo cosa succede con 2 punti: 21 VC-dimension: Esempio
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007
 RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
Ricerca Operativa e Logistica
 Ricerca Operativa e Logistica Dott. F.Carrabs e Dott.ssa M.Gentili A.A. 2011/2012 Lezione 10: Variabili e vincoli logici Variabili logiche Spesso nei problemi reali che dobbiamo affrontare ci sono dei
Ricerca Operativa e Logistica Dott. F.Carrabs e Dott.ssa M.Gentili A.A. 2011/2012 Lezione 10: Variabili e vincoli logici Variabili logiche Spesso nei problemi reali che dobbiamo affrontare ci sono dei
Ottimizzazione nella gestione dei progetti Capitolo 4: la gestione dei costi (Programmazione multimodale): formulazioni
 Ottimizzazione nella gestione dei progetti Capitolo 4: la gestione dei costi (Programmazione multimodale): formulazioni CARLO MANNINO Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica
Ottimizzazione nella gestione dei progetti Capitolo 4: la gestione dei costi (Programmazione multimodale): formulazioni CARLO MANNINO Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Produzione e forza lavoro
 Produzione e forza lavoro Testo Un azienda produce i modelli I, II e III di un certo prodotto a partire dai materiali grezzi A e B, di cui sono disponibili 4000 e 6000 unità, rispettivamente. In particolare,
Produzione e forza lavoro Testo Un azienda produce i modelli I, II e III di un certo prodotto a partire dai materiali grezzi A e B, di cui sono disponibili 4000 e 6000 unità, rispettivamente. In particolare,
TSP con eliminazione di sottocicli
 TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 3 5 7-8 9 57
TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 3 5 7-8 9 57
Informatica. Rappresentazione dei numeri Numerazione binaria
 Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Informatica Rappresentazione dei numeri Numerazione binaria Sistemi di numerazione Non posizionali: numerazione romana Posizionali: viene associato un peso a ciascuna posizione all interno della rappresentazione
Problemi di localizzazione impianti
 Problemi di localizzazione impianti Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 2 Dicembre 2014 Ricerca Operativa 2 Laurea
Problemi di localizzazione impianti Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 2 Dicembre 2014 Ricerca Operativa 2 Laurea
TSP con eliminazione di sottocicli
 TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 7-8 9 7 9-8 79
TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 7-8 9 7 9-8 79
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
CPM - PERT CPM - PERT. Rappresentazione di un progetto. Gestione di un progetto. Critical Path Method Project Evaluation and Review Technique
 CPM - PERT CPM - PERT CPM e PERT sono metodologie per la gestione di progetti composti da più attività in cui esistano relazioni di precedenza. Critical Path Method Project Evaluation and Review Technique
CPM - PERT CPM - PERT CPM e PERT sono metodologie per la gestione di progetti composti da più attività in cui esistano relazioni di precedenza. Critical Path Method Project Evaluation and Review Technique
Database. Si ringrazia Marco Bertini per le slides
 Database Si ringrazia Marco Bertini per le slides Obiettivo Concetti base dati e informazioni cos è un database terminologia Modelli organizzativi flat file database relazionali Principi e linee guida
Database Si ringrazia Marco Bertini per le slides Obiettivo Concetti base dati e informazioni cos è un database terminologia Modelli organizzativi flat file database relazionali Principi e linee guida
1 Estensione in strategia mista di un gioco
 AVVERTENZA: Di seguito trovate alcuni appunti, poco ordinati e poco formali, che uso come traccia durante le lezioni. Non sono assolutamente da considerarsi sostitutivi del materiale didattico. Riferimenti:
AVVERTENZA: Di seguito trovate alcuni appunti, poco ordinati e poco formali, che uso come traccia durante le lezioni. Non sono assolutamente da considerarsi sostitutivi del materiale didattico. Riferimenti:
Sequenziamento a minimo costo di commutazione in macchine o celle con costo lineare e posizione home (In generale il metodo di ottimizzazione
 Sequenziamento a minimo costo di commutazione in macchine o celle con costo lineare e posizione home (In generale il metodo di ottimizzazione presentato in questo file trova la seq. a costo minimo per
Sequenziamento a minimo costo di commutazione in macchine o celle con costo lineare e posizione home (In generale il metodo di ottimizzazione presentato in questo file trova la seq. a costo minimo per
Algoritmi e strutture dati. Codici di Huffman
 Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
A intervalli regolari ogni router manda la sua tabella a tutti i vicini, e riceve quelle dei vicini.
 Algoritmi di routing dinamici (pag.89) UdA2_L5 Nelle moderne reti si usano algoritmi dinamici, che si adattano automaticamente ai cambiamenti della rete. Questi algoritmi non sono eseguiti solo all'avvio
Algoritmi di routing dinamici (pag.89) UdA2_L5 Nelle moderne reti si usano algoritmi dinamici, che si adattano automaticamente ai cambiamenti della rete. Questi algoritmi non sono eseguiti solo all'avvio
Programmazione dinamica
 Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
Rappresentazione grafica di entità e attributi
 PROGETTAZIONE CONCETTUALE La progettazione concettuale, ha il compito di costruire e definire una rappresentazione corretta e completa della realtà di interesse, e il prodotto di tale attività, è lo schema
PROGETTAZIONE CONCETTUALE La progettazione concettuale, ha il compito di costruire e definire una rappresentazione corretta e completa della realtà di interesse, e il prodotto di tale attività, è lo schema
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
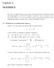 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
PROVA FINALE V. AULETTA G. PERSIANO ALGORITMI II - -MAGIS INFO
 PROVA FINALE V. AULETTA G. PERSIANO ALGORITMI II - -MAGIS INFO 1. Load Balancing Un istanza del problema del load balancing consiste di una sequenza p 1,..., p n di interi positivi (pesi dei job) e un
PROVA FINALE V. AULETTA G. PERSIANO ALGORITMI II - -MAGIS INFO 1. Load Balancing Un istanza del problema del load balancing consiste di una sequenza p 1,..., p n di interi positivi (pesi dei job) e un
Scheduling della CPU. Sistemi multiprocessori e real time Metodi di valutazione Esempi: Solaris 2 Windows 2000 Linux
 Scheduling della CPU Sistemi multiprocessori e real time Metodi di valutazione Esempi: Solaris 2 Windows 2000 Linux Sistemi multiprocessori Fin qui si sono trattati i problemi di scheduling su singola
Scheduling della CPU Sistemi multiprocessori e real time Metodi di valutazione Esempi: Solaris 2 Windows 2000 Linux Sistemi multiprocessori Fin qui si sono trattati i problemi di scheduling su singola
Informatica 3. Informatica 3. LEZIONE 10: Introduzione agli algoritmi e alle strutture dati. Lezione 10 - Modulo 1. Importanza delle strutture dati
 Informatica 3 Informatica 3 LEZIONE 10: Introduzione agli algoritmi e alle strutture dati Modulo 1: Perchè studiare algoritmi e strutture dati Modulo 2: Definizioni di base Lezione 10 - Modulo 1 Perchè
Informatica 3 Informatica 3 LEZIONE 10: Introduzione agli algoritmi e alle strutture dati Modulo 1: Perchè studiare algoritmi e strutture dati Modulo 2: Definizioni di base Lezione 10 - Modulo 1 Perchè
UD 3.4b: Trattabilità e Intrattabilità. Dispense, cap. 4.2
 UD 3.4b: Trattabilità e Intrattabilità Dispense, cap. 4.2 Problemi Intrattabili Esistono problemi che, pur avendo un algoritmo di soluzione, non forniranno mai una soluzione in tempi ragionevoli nemmeno
UD 3.4b: Trattabilità e Intrattabilità Dispense, cap. 4.2 Problemi Intrattabili Esistono problemi che, pur avendo un algoritmo di soluzione, non forniranno mai una soluzione in tempi ragionevoli nemmeno
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
b i 1,1,1 1,1,1 0,1,2 0,3,4
 V o Appello // RICERCA OPERATIVA - Corso A (a.a. 9/) Nome Cognome: Corso di Laurea: L C6 LS LM Matricola: ) Si consideri il problema di flusso di costo minimo in figura. Si verifichi se il flusso ammissibile
V o Appello // RICERCA OPERATIVA - Corso A (a.a. 9/) Nome Cognome: Corso di Laurea: L C6 LS LM Matricola: ) Si consideri il problema di flusso di costo minimo in figura. Si verifichi se il flusso ammissibile
Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005. Lezione 11
 Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005 Docente: Ugo Vaccaro Lezione 11 In questa lezione vedremo alcune applicazioni della tecnica greedy al progetto di algoritmi on-line. Vediamo
Algoritmi e Strutture Dati II: Parte B Anno Accademico 2004-2005 Docente: Ugo Vaccaro Lezione 11 In questa lezione vedremo alcune applicazioni della tecnica greedy al progetto di algoritmi on-line. Vediamo
ALGEBRA DELLE PROPOSIZIONI
 Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Università di Salerno Fondamenti di Informatica Corso di Laurea Ingegneria Corso B Docente: Ing. Giovanni Secondulfo Anno Accademico 2010-2011 ALGEBRA DELLE PROPOSIZIONI Fondamenti di Informatica Algebra
Corso di Informatica
 Corso di Informatica Modulo T3 1-Sottoprogrammi 1 Prerequisiti Tecnica top-down Programmazione elementare 2 1 Introduzione Lo scopo di questa Unità è utilizzare la metodologia di progettazione top-down
Corso di Informatica Modulo T3 1-Sottoprogrammi 1 Prerequisiti Tecnica top-down Programmazione elementare 2 1 Introduzione Lo scopo di questa Unità è utilizzare la metodologia di progettazione top-down
Sono casi particolari di MCF : SPT (cammini minimi) non vi sono vincoli di capacità superiore (solo x ij > 0) (i, j) A : c ij, costo di percorrenza
 Il problema di flusso di costo minimo (MCF) Dati : grafo orientato G = ( N, A ) i N, deficit del nodo i : b i (i, j) A u ij, capacità superiore (max quantità di flusso che può transitare) c ij, costo di
Il problema di flusso di costo minimo (MCF) Dati : grafo orientato G = ( N, A ) i N, deficit del nodo i : b i (i, j) A u ij, capacità superiore (max quantità di flusso che può transitare) c ij, costo di
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
mese 1 2 3 4 5 richiesta 6000 7000 8000 9500 11000
 1.7 Servizi informatici. Un negozio di servizi informatici stima la richiesta di ore di manutenzione/consulenza per i prossimi cinque mesi: mese 1 2 3 4 5 richiesta 6000 7000 8000 9500 11000 All inizio
1.7 Servizi informatici. Un negozio di servizi informatici stima la richiesta di ore di manutenzione/consulenza per i prossimi cinque mesi: mese 1 2 3 4 5 richiesta 6000 7000 8000 9500 11000 All inizio
2 + (σ2 - ρσ 1 ) 2 > 0 [da -1 ρ 1] b = (σ 2. 2 - ρσ1 σ 2 ) = (σ 1
![2 + (σ2 - ρσ 1 ) 2 > 0 [da -1 ρ 1] b = (σ 2. 2 - ρσ1 σ 2 ) = (σ 1 2 + (σ2 - ρσ 1 ) 2 > 0 [da -1 ρ 1] b = (σ 2. 2 - ρσ1 σ 2 ) = (σ 1](/thumbs/25/5899888.jpg) 1 PORTAFOGLIO Portafoglio Markowitz (2 titoli) (rischiosi) due titoli rendimento/varianza ( μ 1, σ 1 ), ( μ 2, σ 2 ) Si suppone μ 1 > μ 2, σ 1 > σ 2 portafoglio con pesi w 1, w 2 w 1 = w, w 2 = 1- w 1
1 PORTAFOGLIO Portafoglio Markowitz (2 titoli) (rischiosi) due titoli rendimento/varianza ( μ 1, σ 1 ), ( μ 2, σ 2 ) Si suppone μ 1 > μ 2, σ 1 > σ 2 portafoglio con pesi w 1, w 2 w 1 = w, w 2 = 1- w 1
Macchine a stati finiti. Sommario. Sommario. M. Favalli. 5th June 2007
 Sommario Macchine a stati finiti M. Favalli 5th June 27 4 Sommario () 5th June 27 / 35 () 5th June 27 2 / 35 4 Le macchine a stati si utilizzano per modellare di sistemi fisici caratterizzabili mediante:
Sommario Macchine a stati finiti M. Favalli 5th June 27 4 Sommario () 5th June 27 / 35 () 5th June 27 2 / 35 4 Le macchine a stati si utilizzano per modellare di sistemi fisici caratterizzabili mediante:
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Calcolatori Elettronici A a.a. 2008/2009
 Calcolatori Elettronici A a.a. 2008/2009 PRESTAZIONI DEL CALCOLATORE Massimiliano Giacomin Due dimensioni Tempo di risposta (o tempo di esecuzione): il tempo totale impiegato per eseguire un task (include
Calcolatori Elettronici A a.a. 2008/2009 PRESTAZIONI DEL CALCOLATORE Massimiliano Giacomin Due dimensioni Tempo di risposta (o tempo di esecuzione): il tempo totale impiegato per eseguire un task (include
Macchine a stati finiti. Sommario. Sommario. M. Favalli. Le macchine a stati si utilizzano per modellare di sistemi fisici caratterizzabili mediante:
 Sommario Macchine a stati finiti M. Favalli Engineering Department in Ferrara 4 Sommario (ENDIF) Analisiesintesideicircuitidigitali / 35 (ENDIF) Analisiesintesideicircuitidigitali 2 / 35 4 Le macchine
Sommario Macchine a stati finiti M. Favalli Engineering Department in Ferrara 4 Sommario (ENDIF) Analisiesintesideicircuitidigitali / 35 (ENDIF) Analisiesintesideicircuitidigitali 2 / 35 4 Le macchine
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
La Programmazione Lineare
 4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
Introduzione al MATLAB c Parte 2
 Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
Introduzione al MATLAB c Parte 2 Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 18 gennaio 2008 Outline 1 M-file di tipo Script e Function Script Function 2 Costrutti di programmazione
INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI INTRODUZIONE AGLI ALGORITMI
 INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
INTRODUZIONE AGLI ALGORITMI Prima di riuscire a scrivere un programma, abbiamo bisogno di conoscere un metodo risolutivo, cioè un metodo che a partire dai dati di ingresso fornisce i risultati attesi.
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
La Minimizzazione dei costi
 La Minimizzazione dei costi Il nostro obiettivo è lo studio del comportamento di un impresa che massimizza il profitto sia in mercati concorrenziali che non concorrenziali. Ora vedremo la fase della minimizzazione
La Minimizzazione dei costi Il nostro obiettivo è lo studio del comportamento di un impresa che massimizza il profitto sia in mercati concorrenziali che non concorrenziali. Ora vedremo la fase della minimizzazione
Corso di Calcolo Numerico
 Corso di Calcolo Numerico Dott.ssa M.C. De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Sistemi di Numerazione Sistema decimale La
Corso di Calcolo Numerico Dott.ssa M.C. De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Sistemi di Numerazione Sistema decimale La
Lezioni di Ricerca Operativa. Corso di Laurea in Informatica Università di Salerno. Lezione n 4
 Lezioni di Ricerca Operativa Lezione n 4 - Problemi di Programmazione Matematica - Problemi Lineari e Problemi Lineari Interi - Forma Canonica. Forma Standard Corso di Laurea in Informatica Università
Lezioni di Ricerca Operativa Lezione n 4 - Problemi di Programmazione Matematica - Problemi Lineari e Problemi Lineari Interi - Forma Canonica. Forma Standard Corso di Laurea in Informatica Università
Obiettivi dell Analisi Numerica. Avviso. Risoluzione numerica di un modello. Analisi Numerica e Calcolo Scientifico
 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p. 3/43 M. Annunziato, DIPMAT Università di Salerno - Queste note non sono esaustive ai fini del corso p.
Complessità Computazionale
 Complessità Computazionale Analisi Algoritmi e pseudocodice Cosa significa analizzare un algoritmo Modello di calcolo Analisi del caso peggiore e del caso medio Esempio di algoritmo in pseudocodice INSERTION
Complessità Computazionale Analisi Algoritmi e pseudocodice Cosa significa analizzare un algoritmo Modello di calcolo Analisi del caso peggiore e del caso medio Esempio di algoritmo in pseudocodice INSERTION
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Calcolatori: Algebra Booleana e Reti Logiche
 Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Calcolatori: Algebra Booleana e Reti Logiche 1 Algebra Booleana e Variabili Logiche I fondamenti dell Algebra Booleana (o Algebra di Boole) furono delineati dal matematico George Boole, in un lavoro pubblicato
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
I.I.S. Primo Levi Badia Polesine A.S. 2012-2013
 LGEBR DI BOOLE I.I.S. Primo Levi Badia Polesine.S. 2012-2013 Nel secolo scorso il matematico e filosofo irlandese Gorge Boole (1815-1864), allo scopo di procurarsi un simbolismo che gli consentisse di
LGEBR DI BOOLE I.I.S. Primo Levi Badia Polesine.S. 2012-2013 Nel secolo scorso il matematico e filosofo irlandese Gorge Boole (1815-1864), allo scopo di procurarsi un simbolismo che gli consentisse di
Epoca k Rata Rk Capitale Ck interessi Ik residuo Dk Ek 0 S 0 1 C1 Ik=i*S Dk=S-C1. n 0 S
 L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
Ottimizzazione delle interrogazioni (parte I)
 Ottimizzazione delle interrogazioni I Basi di Dati / Complementi di Basi di Dati 1 Ottimizzazione delle interrogazioni (parte I) Angelo Montanari Dipartimento di Matematica e Informatica Università di
Ottimizzazione delle interrogazioni I Basi di Dati / Complementi di Basi di Dati 1 Ottimizzazione delle interrogazioni (parte I) Angelo Montanari Dipartimento di Matematica e Informatica Università di
Ricerca Operativa A.A. 2007/2008
 Ricerca Operativa A.A. 2007/2008 9. Cenni su euristiche e metaeuristiche per ottimizzazione combinatoria Motivazioni L applicazione di metodi esatti non è sempre possibile a causa della complessità del
Ricerca Operativa A.A. 2007/2008 9. Cenni su euristiche e metaeuristiche per ottimizzazione combinatoria Motivazioni L applicazione di metodi esatti non è sempre possibile a causa della complessità del
Capitolo 3: Ottimizzazione Discreta. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 3: Ottimizzazione Discreta E. Amaldi DEIB, Politecnico di Milano 3.1 Modelli di PLI e PLMI Moltissimi problemi decisionali complessi possono essere formulati o approssimati come problemi di Programmazione
Capitolo 3: Ottimizzazione Discreta E. Amaldi DEIB, Politecnico di Milano 3.1 Modelli di PLI e PLMI Moltissimi problemi decisionali complessi possono essere formulati o approssimati come problemi di Programmazione
(a cura di Francesca Godioli)
 lezione n. 12 (a cura di Francesca Godioli) Ad ogni categoria della variabile qualitativa si può assegnare un valore numerico che viene chiamato SCORE. Passare dalla variabile qualitativa X2 a dei valori
lezione n. 12 (a cura di Francesca Godioli) Ad ogni categoria della variabile qualitativa si può assegnare un valore numerico che viene chiamato SCORE. Passare dalla variabile qualitativa X2 a dei valori
Reti sequenziali sincrone
 Reti sequenziali sincrone Un approccio strutturato (7.1-7.3, 7.5-7.6) Modelli di reti sincrone Analisi di reti sincrone Descrizioni e sintesi di reti sequenziali sincrone Sintesi con flip-flop D, DE, T
Reti sequenziali sincrone Un approccio strutturato (7.1-7.3, 7.5-7.6) Modelli di reti sincrone Analisi di reti sincrone Descrizioni e sintesi di reti sequenziali sincrone Sintesi con flip-flop D, DE, T
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
Logica Numerica Approfondimento 1. Minimo Comune Multiplo e Massimo Comun Divisore. Il concetto di multiplo e di divisore. Il Minimo Comune Multiplo
 Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Prodotto Disponibilità Costo 1 3000 3 2 2000 6 3 4000 4. e rispettando le seguenti regole di composizione delle benzine:
 1.1 Pianificazione degli investimenti. Una banca deve investire C milioni di Euro, e dispone di due tipi di investimento: (a) con interesse annuo del 15%; (b) con interesse annuo del 25%. Almeno 1 di C
1.1 Pianificazione degli investimenti. Una banca deve investire C milioni di Euro, e dispone di due tipi di investimento: (a) con interesse annuo del 15%; (b) con interesse annuo del 25%. Almeno 1 di C
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Sia data la rete di fig. 1 costituita da tre resistori,,, e da due generatori indipendenti ideali di corrente ed. Fig. 1
 Analisi delle reti 1. Analisi nodale (metodo dei potenziali dei nodi) 1.1 Analisi nodale in assenza di generatori di tensione L'analisi nodale, detta altresì metodo dei potenziali ai nodi, è un procedimento
Analisi delle reti 1. Analisi nodale (metodo dei potenziali dei nodi) 1.1 Analisi nodale in assenza di generatori di tensione L'analisi nodale, detta altresì metodo dei potenziali ai nodi, è un procedimento
