+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
|
|
|
- Aurelia Casini
- 8 anni fa
- Visualizzazioni
Transcript
1 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a di tutti i termini della successione. Questa operazione formale è detta serie (infinita) di termine generale, e viene anche indicata con la scrittura + P Nel seguito farà comodo avere la possibilità di cambiare l indice della sommatoria, in modo da iniziare a sommare da valori diversi da. Se risulta più utile avere a che fare con sommatorie che iniziano da 4, èsufficiente cambiare n in m = n +3, per ottenere la scrittura = m=4 a m 3. Inoltre, capiterà di avere a che fare con successioni { } definite per ogni n 0, ed in quei casi tratteremo con n=0 = a 0 + a + a Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento: i) Per ogni n fissato, calcoliamo la somma dei primi n termini della serie s n = n a k = a + a a k. ii) Abbiamo in questo modo ottenuto la successione {s n }, icuiterminisono 37
2 38 CAPITOLO 3. SERIE s = s 2 = P P 2 a k = a a k = a + a 2... P s n = n a k = a + a e questa successione viene detta successione delle somme parziali della serie + P. È utile osservare che la costruzione della {s n } apartiredalla{ } avviene in modo iterativo, perchè s n = s n + per ogni n 2. Questo permette di affermare che ogni successione {S n } è la successione delle somme parziali di una ben precisa + P A n ; basta infatti utilizzare A = S, e A n = S n S n per n 2. Definizione 3. Una serie + P èdettaconvergente, divergente o irregolare,aseconda che lo sia la sua successione delle somme parziali. Determinare il carattere di una serie significa stabilire a quale delle tre precedenti categorie appartenga. Le serie convergenti o divergenti sono dette regolari. Definizione 3.2 Per le serie convergenti, il lim s n = s R è detto somma dellaserie,edinquestocasosiscrive s = + P. Esempio La serie di termine generale costante = c R per ogni n ha ovviamente successione delle somme parziali s n = nc, equindiè convergente con somma 0 nel caso c =0, divergente a + se c>0, e divergente a se c<0. N Esempio 2 È immediato calcolare {s n} nel caso della serie di termine generale =( ) n. Infatti s =, s 2 = +=0,s 3 = + =,...Poichè la somma di due termini consecutivi dà risultato nullo, la successione {s n } assume i valori e 0, a seconda che n sia dispari o pari. La serie è perciò irregolare. N Esempio 3 La serie di termine generale = n è divergente a +, perchè hasommeparziali n(n +) s n =. N 2 In questi esempi ci è stato possibile ricavare la successione {s n } in modo esplicito, ma questo può essere, in generale, un compito molto arduo, se non impossibile.
3 3.2. PROPRIETÀ GENERALI Proprietà generali Nell affrontare lo studio di una serie ci troviamo a cercare una risposta per: Problema A Determinare il carattere della serie. Problema B Se la serie è convergente, calcolarne la somma. Dare una risposta al secondo problema può essereestremamentedifficile, come si può notare dalla Proposizione 3.3 Se i termini delle serie + P e + P b n differiscono solo per un numero finito di indici, le serie hanno lo stesso carattere. Dim. Itermini e b n coincidono per ogni n N, per cui le rispettive somme parziali di posto N + m soddisfano s N+m t N+m = = = N+m à N N N+m a k N+m a k + k=n N a k b k = a k! b k = C. à N N+m b k + k=n b k! Così, la differenza s n t n èdefinitivamente costante, e le successioni {s n } e {t n } sono entrambe convergenti, o divergenti, o irregolari. Dalla dimostrazione di questa Proposizione si nota che, mentre la modifica di un numero finito di termini di una serie convergente non ne cambia il carattere, questa operazione può rendere molto arduo il compito di calcolarne la somma. Per questo motivo ci dedichiamo, nel seguito, a cercare criteri che permettano di rispondere al Problema A. Unodiquesticriteriè: Teorema 3.4 Se la serie + P converge, si ha lim =0. Dim. Per ipotesi la successione delle somme parziali {s n } converge al limite finito s. Poichè = s n s n, per n + abbiamo s s =0. Il teorema fornisce una condizione necessaria affinchè una serie converga, e ci dà la possibilità di individuare facilmente alcune serie che non convergono. Esempio 4 Le serie di termine generale =,b n =( ) n,c n = n viste negli esempi precedenti non convergono. Così pure + P 2 /n non converge, in quanto 2 /n 6= 0. N La condizione lim =0nonèperòsufficiente per garantire la convergenza di una serie, e quindi il teorema ha un applicazione limitata. Può infatti accadere che il termine generale tenda a zero senza che la serie converga.
4 40 CAPITOLO 3. SERIE Esempio 5 + P n ++ n. Ovviamente 0; inoltre, moltiplicando e dividendo per ( n + n) troviamo subito che = n + n. Così s n = a 2 + a = ( n + n)+( n n ) ( 3 2) + ( 2 ) = n + + equindilaseriedivergea+. N Un risultato più completo del precedente fornisce una condizione siecessaria che sufficiente per la convergenza di una serie. Teorema 3.5 (Criterio di Cauchy) La serie + P converge se e solo se è soddisfatta la condizione di Cauchy per le serie n+p P ε > 0 n = n(ε) : n n, p = a < ε. k k=n+ Dim. Poichè la convergenza della serie equivale alla convergenza della successione delle somme parziali {s n }, possiamo utilizzare il Teorema 2. per concludere che la serie converge se e solo se la {s n } soddisfa la condizione di Cauchy ε > 0 n = n(ε) : n, m n = s m s n < ε, e chiaramente possiamo pensare che si<m= n + p. Così n+p n ε > s m s n = a k a = k cioè latesi. n+p k=n+ Quest ultimo teorema è di scarso utilizzo pratico. Per questo motivo decidiamo di cercare condizioni che siano magari solo sufficienti, ma più maneggevoli da applicare. 3.3 Convergenza assoluta Spesso si fa riferimento alla convergenza di una serie come alla convergenza semplice, per marcare la distinzione con la seguente proprietà. Definizione 3.6 La serie + P è assolutamente convergente se è convergente la serie + P. Ovviamente, lozione di convergenza (semplice) e quella di convergenza assoluta coincidono nel caso i termini della serie siano tutti (o almeno definitivamente) dello stesso segno. Queste due nozioni sono legate dal a k
5 3.4. SERIE A TERMINI DI SEGNO COSTANTE (I) 4 Teorema 3.7 La convergenza assoluta implica la convergenza. Dim. Se + P è convergente, necessariamente soddisfa la condizione di Cauchy. Mostriamo che anche la + P soddisfa la stessa condizione; ciòsaràsufficiente per garantirne la convergenza. n+p P Per ε > 0 fissato, esiste un indice n che garantisce che se n n esep, allora a k k=n+ < ε. Così, per gli stessi n e p abbiamo n+p n+p a a k k < ε k=n+ cioè la condizione di Cauchy per la serie + P. k=n+ L enunciato del Teorema 3.7 non è invertibile, nel senso che esistono serie numeriche semplicemente convergenti, mon assolutamente convergenti. Perciò, la convergenza assoluta rappresenta una condizione sufficiente, mon necessaria, per la convergenza (semplice) di una serie. Esempio 6 Non siamo ancora in grado di dimostrarlo, ma più avanti (Proposizione 3.3 ed Esempio 4) vedremo che la serie ( ) n+ n = converge semplicemente, mon assolutamente. N Esempio 7 Più avanti (Esempio 0) saremo anche in grado di dimostrare che la + P cos n n 2, icuiterminihannounsegnodifficile da determinare, èassolutamenteconvergente,equindi convergente. N Nel prossimo paragrafo scopriremo che se il termine ha (almeno definitivamente) segno costante, è possibile ricavare alcune informazioni su + P ; la stessa coson è in generale possibile per serie il cui termine generale ha segno arbitrario. Per queste ultime, il Teorema 3.7 costituisce la più semplice condizione (seppur solo sufficiente) di convergenza. 3.4 Serie a termini di segno costante (I) Consideriamo ora serie + P, il cui termine generale ha segno costante. pensiamo di avere 0. Per comodità, Teorema 3.8 Se 0 per ogni n, la serie + P è regolare. Più precisamente: la serie è converge oppure diverge a +.
6 42 CAPITOLO 3. SERIE Dim. Abbiamo s n+ = s n + + s n n e quindi la successione {s n } è monotònon-decrescente, quindi convergente (se limitata) oppure divergente a + (vd. par.2.4). Con un comprensibile abuso di notazione, per queste serie scriviamo =+ oppure nelcasosiano,rispettivamente,divergentioconvergenti. < + Teorema 3.9 (Criterio del confronto) Date le serie + P e + P b n, con 0 b n per ogni n, siha: se se + P + P =+ b n < + allora allora + P + P b n =+ ; < +. P Dim. Le successioni delle somme parziali s n = n P a k e t n = n b k soddisfano s n t n. Corollario 3.0 Se esistono due costanti C, c > 0 per la quali c b n C definitivamente le serie + P e + P b n sono entrambe convergenti, o entrambe divergenti. In particolare, questo vale se b n. Osservazione Per quanto detto nella Proposizione 3.3, le tesi del Teorema 3.9 e del Corollario 3.0 rimangono valide anche se le ipotesi non sono verificate per ogni n, ma lo sono definitivamente. Il Criterio del confronto, ed il suo corollario, sono strumenti estremamente utili per stabilire il comportamento di una serie a termini non-negativi, perchè permettono di ricondurre il problema della convergenza di una serie + P b n, in cui b n è difficile da trattare, a quello della convergenza di una serie + P in cui ha un comportamento confrontabile con quello di b n, ma un aspetto più semplice. Chiaramente, l utilizzabilità diquesticriteriètantopiùampiaquantopiùè ricco l elenco di serie campione di cui è noto il comportamento; il prossimo paragrafo contiene lo studio di alcune serie particolari. Concludiamo questa prima sezione di risultati teorici per serie a termini non-negativi con un risultato che lega serie ed integrali impropri.
7 3.5. ALCUNE SERIE CAMPIONE 43 Teorema 3. (Criterio integrale) Sia f :[, + ) R una funzione non-negativa e monotòna non-crescente. Allora Z + f(x)dx e f(n) sono contemporaneamente convergenti oppure divergenti. Dim. Per ogni k intero l integrale di f esteso all intervallo [k, k + ] soddisfa f(k +) Z k+ perchè f è monotòna e non-negativa. Sommando n n s n f() = f(k) = f(k +) k=2 k f(x)dx f(k) Z n n f(x)dx f(k) =s n s n. Da qui segue la tesi, perchè R n f(x)dx R + f(x)dx in quanto f ha segno costante. 3.5 Alcune serie campione Riportiamo alcune Proposizioni che descrivono il comportamento di alcune serie. Le dimostrazioni di questi risultati possono essere ottenute anche in modo diverso da quello proposto, utilizzando icriterifin quiincontrati. Proposizione 3.2 (Serie geometrica) La serie n=0 q n =+q + q 2 + q , q R èdettaserie geometrica di ragione q. Questa serie converge alla somma diverge a + se q, ed è irregolare se q. q nel caso q <, Dim. La serie ha termini non-negativi solo nel caso q 0. Nel caso q = abbiamo chiaramente s n = n + + ; inoltre, anche nel caso q 6= siamo in grado di calcolare esplicitamente la successione delle somme parziali s n = s n (q) =+q q n = ( + q qn )( q) q = qn+. q Se ne ricava che lim s n(q) = + se q q se se q
8 44 CAPITOLO 3. SERIE da cui segue la tesi. Osservazione In modo simile si ottiene che, per q <, q n = qn n=n q. Osservazione Una parte delle risposte fornite da questa Proposizione può anche essere ottenuta in altro modo. Infatti, dalla divergenza della serie per q = si ottiene, per il Criterio del confronto, chelaseriedivergea+ per ogni q. Per q non ci può essere convergenza, perchè il termine generale non tende a zero (vd. Teorema 3.4). + P Esempio 8 La Proposizione 3.2 può essere utilizzata per scrivere sotto forma di frazione un numero periodico. Ad esempio 0, 37 = 0, = = = = = = n=0 0 2 n. N Esempio 9 In modo simile, abbiamo: 0, 38 = 0, = = = = = n=0 0 n. N Proposizione 3.3 (Serie armonica) La serie diverge a +. n = Dim. La funzione f(x) = x, x, è positiva e decrescente, e R + (/x) dx non converge. Per il Criterio integrale (Teorema 3.) abbiamo la tesi. Osservazione La serie armonica fornisce un altro esempio di serie in cui la condizione lim = 0nonèsufficiente per garantire la convergenza della serie (vd. Teorema 3.4 ed Esempio 5).
9 3.5. ALCUNE SERIE CAMPIONE 45 Proposizione 3.4 (Serie armonica generalizzata) La serie n p =+ 2 p (p R) 3p converge se e solo se p>. Per p diverge a +. Dim. È una serie a termini positivi, quindi convergente oppure divergente a + (Teor.3.8). Se p 0 il termine generale non tende a 0, e quindi la serie diverge (Teor. 3.4). Se p>0, applichiamo il Criterio integrale (Teor. 3.) alla funzione positiva e decrescente f(x) = x p, x. Esempio 0 La serie + P cos n n 2 incontratell Es.7 è assolutamente convergente, perchè cos n n 2 n 2.. N Esempio Il termine generale della serie di Mengoli + P soddisfa la relazione n(n +) n(n +), e quindi, per il Corollario 3.0 e la Proposizione 3.4 la serie converge. In n2 realtà, di questa serie siamo anche in grado di calcolare la somma. Infatti il suo termine generale può essere scritto come = n(n +) = n n + per cui µ s n = µ µ µ n n + = n n + = n + per via delle cancellazioni. Così, s n, e la serie di Mengoli ha somma. (Somme finite di questo tipo, in cui tutti i termini tranne il primo e l ultimo si cancellano, sono anche dette somme telescopiche.) A titolo di curiosità: è possibile dimostrare (mon con le tecniche di cui disponiamo ora) che + P n 2 = π2 6. N Sempre utilizzando il Criterio integrale (Teor. 3.) è possibile ottenere il seguente risultato, che estende quanto detto per la serie armonica generalizzata. Proposizione 3.5 La serie n=2 n p (log n) q p, q R converge solo nei casi: p >, q qualsiasi oppure p =,q >.
10 46 CAPITOLO 3. SERIE 3.6 Serie a termini di segno costante (II) Il Criterio integrale non è l unico strumento che ci permette di stabilire se una serie a termini non-negativi converge. Tra le varie altre condizioni, segnaliamo le più note. Teorema 3.6 (Criterio del Rapporto) Sia + P una serie a termini positivi. ) Se lim sup + <, la serie + P converge. ) Se + definitivamente, la serie + P diverge. Dim. Se lim sup abbiamo + + < δ se n n = n(δ). Perciò <, esiste δ (0, ) per cui lim sup < δ < δ 2 2 <...<δ n n + < δ < e, per il Teor. 2.5, n>n Così èdefinitivamente maggiorabile con il termine generale di una serie geometrica convergente, e quindi + P converge. Se invece + per ogni n n, la successione{ } non può tendere a zero. Corollario 3.7 Sia + P una serie a termini positivi, per la quale esiste [0, + ]. Allora: + lim = ` Osservazione + P Quando lim sup ) se `<, la serie + P converge; ) se `>, la serie + P diverge. +,p R, soddisfano questa condizione. np Esempio 2 La serie n=0 x n n! = questo criterio è inconcludente. Ad esempio, tutte le =+x + x2 2! + x3 3! +..., x R è detta serie esponenziale. Possiamo mostrare che converge assolutamente per ogni x R. Se x =0è ovvio, mentre per x 6= 0poniamo = x n /n! ed abbiamo + n! (n +)! x n = = x n+ x n + 0 <.
11 3.6. SERIE A TERMINI DI SEGNO COSTANTE (II) 47 Questaseriedeveilnomealfattochesipuòdimostrare n=0 x n n! = ex dove e è il numero di Nepero. Perciò µ lim + t = e = t + t n!. n=0. N Teorema 3.8 (Criterio della Radice) Sia + P λ =limsup n an. Allora: una serie a termini non-negativi, e sia ) se λ <, la serie + P converge; ) se λ >, la serie + P diverge. Dim. Se λ <, esiste µ (0, ) per cui lim sup n an <µse n n = n(δ). Perciò n an <µ< e, per il Teor. 2.5, abbiamo <µ n n>n. Così èdefinitivamente maggiorabile con il termine generale di una serie geometrica convergente, e quindi + P converge. Se invece λ >, dalla Definizione 2.2 segue che esiste una sottosuccessione di n ª che converge a λ, e quindi { } non può tendere a 0. Corollario 3.9 Sia + P a termini non-negativi, e supponiamo esista [0, + ]. Allora: lim n an = λ ) se λ <, la serie + P converge; ) se λ >, la serie + P diverge. Osservazione Anche in questo caso, se λ = il criterio è inconcludente. Tutte le + P soddisfano questa condizione.,p R, np
12 48 CAPITOLO 3. SERIE Esempio 3 La serie + P Invece la serie + P (n +) n µ n n converge, in quanto 2n + n an = n 2n + 2. e 3n diverge, perchè n = n + e 3 +. N Osservazione Il Criterio della Radice è spesso più difficile da utilizzare rispetto al Criterio del Rapporto, ma ha uno spettro di applicabilità maggiore. Questo significa che se il Teorema 3.6 fornisce una risposta, la (stessa) risposta si ottiene con il Teorema 3.8; se invece il Criterio della Radice non dà risposta, lo stesso accade con il Criterio del Rapporto. La dimostrazione di questo fatto esula dai limiti che ci poniamo per questi appunti. 3.7 Serie a termini di segno alternato Tornando ad esaminare serie i cui termini non hanno segno costante, c è un caso (molto particolare)perilqualesiriesceadottenereuncriteriodiconvergenzadiversodaquellochecoinvolge la convergenza assoluta (Teorema 3.7). Si tratta di serie del tipo ( ) n = a a 2 + a 3 a dove > 0perognin. Tutti i termini di indice dispari sono non-negativi, e quelli di indice pari sono non-positivi; sono dette serie a termini di segno alternato. Ovviamente la convergenza assoluta, cioè la convergenza di + P, implica la convergenza della + P ( ) n ; per ottenere la convergenza semplice vi èperò anche un altro criterio. Teorema 3.20 (Criterio di Leibniz) Sia { } una successione positiva, non-crescente e infinitesima, cioè: Allora la serie + P ( ) n converge. ) 0<+ per ogni n; ) lim =0. Inoltre, la differenza (in valore assoluto) tra la somma s e la somma parziale n-sima s n non supera il valore assoluto del primo termine trascurato, cioè: s s n + n. Dim. La successione {s 2n+ } delle somme parziali di indice dispari è non-crescente, perchè s 2n+ = s 2n (a 2n a 2n+ ) s 2n ; allo stesso modo si dimostra che {s 2n } è non-decrescente. Così
13 3.8. PROPRIETÀ COMMUTATIVA 49 s 2 s 4... s 2n s 2n+... s 3 s e questo mostra che le due successioni {s 2n+ } e {s 2n } sono monotòne e limitate, quindi convergenti. Inoltre s 2n+ s 2n = a 2n+ 0 e quindi {s 2n+ } e {s 2n } convergono, la prima per eccesso e la seconda per difetto, allo stesso limite s. Infine e 0 s s 2n s 2n+ s 2n = a 2n+ da cui segue la tesi. 0 s 2n+ s s 2n+ s 2n+2 = a 2n+2 Esempio 4 La serie + P ( ) n n converge, perchè n perciò giustificato quanto affermato nell Esempio 6. decresce monotonamente a 0. Abbiamo N 3.8 Proprietà commutativa In questo paragrafo ci occupiamo dei riordinamenti di una serie. Data la serie + P un suo riordinamento èlaserie + P b n che si ottiene rimescolando l ordine dei termini. Questo significa che tra i termini { } ed i termini {b n } vi è una corrispondenza biunivoca, ed è solo cambiato l ordine in cui compaiono. In modo più formale, esiste una corrispondenza biunivoca φ : N N tra gli indici, ed i termini delle serie sono legati dalla relazione b n = a φ(n). Siamo interessati a rispondere alla domanda: Per quali serie convergenti + P possiamo garantire che ogni riordinamento + P b n è ancora convergente e ha la stessa somma? Le serie per cui questo accade sono dette incondizionatamente convergenti. Senza dimostrazioni, riportiamo il più significativo risultato in questa direzione. Teorema 3.2 (Dirichlet) La serie + P è incondizionatamente convergente se e solo se è assolutamente convergente.
14 50 CAPITOLO 3. SERIE Segnaliamo che una della due implicazioni di questo teorema segue dall elegante Teorema 3.22 (Riemann) Sia + P una serie che converge semplicemente, mon assolutamente. Allora, comunque fissati α β +, la serie data ammette un riordinamento + P b n la cui successione delle somme parziali {t n } ammette α come limite inferiore e β come limite superiore.
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
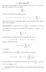 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Alcuni complementi sulle successioni
 Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Analisi Matematica 3 appunti
 Corso di Laurea in Statistica Matematica e trattamento Informatico dei Dati Analisi Matematica 3 appunti Francesca Astengo Università di Genova, A.A. 20/202 Indice Capitolo. Serie numeriche. Brevi richiami
Corso di Laurea in Statistica Matematica e trattamento Informatico dei Dati Analisi Matematica 3 appunti Francesca Astengo Università di Genova, A.A. 20/202 Indice Capitolo. Serie numeriche. Brevi richiami
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Metodi risolutivi per le disequazioni algebriche
 Metodi risolutivi per le disequazioni algebriche v.scudero Una disequazioni algebrica si presenta in una delle quattro forme seguenti: () P( () P( (3) P( () P( essendo P( un polinomio in. Noi studieremo
Metodi risolutivi per le disequazioni algebriche v.scudero Una disequazioni algebrica si presenta in una delle quattro forme seguenti: () P( () P( (3) P( () P( essendo P( un polinomio in. Noi studieremo
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
Appunti di Analisi Matematica 1. Docente: Klaus Engel. Università degli Studi dell Aquila Facoltà di Ingegneria A.A. 2011/12
 Appunti di Analisi Matematica Docente: Klaus Engel Università degli Studi dell Aquila Facoltà di Ingegneria A.A. / http://univaq.it/~engel ( = %7E) (Versione del 4 dicembre ) Note scritte in collaborazione
Appunti di Analisi Matematica Docente: Klaus Engel Università degli Studi dell Aquila Facoltà di Ingegneria A.A. / http://univaq.it/~engel ( = %7E) (Versione del 4 dicembre ) Note scritte in collaborazione
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
Prodotto libero di gruppi
 Prodotto libero di gruppi 24 aprile 2014 Siano (A 1, +) e (A 2, +) gruppi abeliani. Sul prodotto cartesiano A 1 A 2 definiamo l operazione (x 1, y 1 ) + (x 2, y 2 ) := (x 1 + x 2, y 1 + y 2 ). Provvisto
Prodotto libero di gruppi 24 aprile 2014 Siano (A 1, +) e (A 2, +) gruppi abeliani. Sul prodotto cartesiano A 1 A 2 definiamo l operazione (x 1, y 1 ) + (x 2, y 2 ) := (x 1 + x 2, y 1 + y 2 ). Provvisto
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli. 03 - Equazioni differenziali lineari omogenee a coefficienti costanti.
 Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
Capitolo 2. Serie Numeriche
 Capitolo 2 Serie Numeriche Iniziamo ricordando la nozione di successione e le operazioni definibili tra successioni. Questo permetterà di poter definire, con una certa semplicità la nozione di somma infinita
Capitolo 2 Serie Numeriche Iniziamo ricordando la nozione di successione e le operazioni definibili tra successioni. Questo permetterà di poter definire, con una certa semplicità la nozione di somma infinita
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
SOMMARIO. 13.1 I radicali pag. 3. 13.2 I radicali aritmetici pag. 5. 13.3 Moltiplicazione e divisione fra radicali aritmetici pag.
 SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
LA FUNZIONE INTEGRALE
 LA FUNZIONE INTEGRALE MAGLIOCURIOSO & CAMILLO magliocurioso@hotmail.it Sommario. In questa breve dispensa ho semplicementrascritto in L A TEX il contenuto di questa discussione: http://www.matematicamente.it/forum/
LA FUNZIONE INTEGRALE MAGLIOCURIOSO & CAMILLO magliocurioso@hotmail.it Sommario. In questa breve dispensa ho semplicementrascritto in L A TEX il contenuto di questa discussione: http://www.matematicamente.it/forum/
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
x ( 3) + Inoltre (essendo il grado del numeratore maggiore del grado del denominatore, d ancora dallo studio del segno),
 6 - Grafici di funzioni Soluzioni Esercizio. Studiare il grafico della funzione f(x) = x x + 3. ) La funzione è definita per x 3. ) La funzione non è né pari, né dispari, né periodica. 3) La funzione è
6 - Grafici di funzioni Soluzioni Esercizio. Studiare il grafico della funzione f(x) = x x + 3. ) La funzione è definita per x 3. ) La funzione non è né pari, né dispari, né periodica. 3) La funzione è
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
7 - Esercitazione sulle derivate
 7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
STRUTTURE ALGEBRICHE
 STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
