Serie numeriche e serie di potenze
|
|
|
- Viviana Moro
- 8 anni fa
- Visualizzazioni
Transcript
1 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima di dare delle definizioni precise facciamo qualche piccolo esperimento Se sommiamo i numeri interi positivi otteniamo Se modifichiamo questa somma nel seguente modo la risposta è meno banale Per trovarla abbiamo bisogno di osservare il comportamento delle somme parziali Notiamo che una parte delle somme cresce verso + mentre l altra descresce verso e dunque il loro comportamento complessivo è indeterminato Se invece sommiamo infiniti zeri In quest ultimo caso il risultato dell operazione di somma infinita è un numero finito C è un esempio più interessante? È chiaro che se vogliamo avere la speranza di trovarne una dobbiamo almeno fare in modo che il termine che via via viene aggiunto tenda a zero Consideriamo per esempio la somma delle potenze positive di : Esiste il limite di questa somma e se esiste siamo in grado di calcolarlo? Nel corso di questo capitolo ci occuperemo proprio di questo genere di problemi Intanto possiamo dare una risposta in questo caso particolare utilizzando un ragionamento geometrico In un quadrato di lato vengono via via ritagliati dei triangoli rettangoli le cui aree corrispondono proprio ai termini della somma che stiamo esaminando
2 4 Roberto Tauraso - Analisi Questi infiniti triangoli esauriscono la superficie del quadrato e dunque la somma infinita delle loro aree è uguale all area totale del quadrato ossia : Definizioni e prime proprietà Precisiamo meglio il linguaggio che intendiamo usare Data una successione di numeri reali {a n } con n 0,,,, la loro somma fino al termine N-esimo è detta somma parziale di ordine N s N a 0 + a + a + + a N Per evitare eventuali fraintendimenti (+ +?) e rendere la scrittura più comoda e sintetica, una somma parziale si può scrivere anche in questo modo s N N dove è il simbolo di sommatoria e rappresenta un ciclo di somme di termini a n con l indice intero n che varia dal numero scritto in basso, 0, al numero scritto in alto, N La successione delle somme parziali {s N } con n 0,,, costituisce la serie dei termini a n Determinare il carattere della serie significa studiare il limite della successione delle somme parziali: In particolare avremo questi tre casi: lim s N N a n a n Carattere di una serie L R la serie converge con somma L a n + o la serie diverge non esiste la serie è indeterminata
3 Serie numeriche e serie di potenze 5 Nel caso si debbano fare operazioni tra serie, dato che sono dei limiti, dovremo fare particolare attenzione Per esempio la seguente serie è evidentemente divergente a + : n + Ora proviamo a fare la seguente operazione n n ( ) Quindi sembra di poter concludere che n ( ) n n n Questo imbarazzante risultato è dovuto al fatto che non ci siamo accorti della presenza di una forma indeterminata (+ ) Le combinazioni lineari di serie si possono però fare quando le serie in gioco sono convergenti: Siano la serie a n e Linearità b n due serie convergenti Allora converge anche (α a n + β b n ) dove c, c R Inoltre (α a n + β b n ) α a n + β b n Concludiamo questa sezione con qualche utile osservazione sul carattere di una serie Intanto è piuttosto semplice convincersi che la convergenza di una serie dipende solo dalla coda dei termini che sommiamo: converge se e solo se converge, a n nn 0 a n dove n 0 è un qualunque numero intero positivo Quindi al fine di determinare il carattere di una serie si possono trascurare i primi termini (anche se questo potrebbe cambiare il valore della somma) Un primo semplice criterio per determinare se una serie non converge è quello di verificare se il termine generico della serie non è infinitesimo Infatti, se la serie converge, la successione delle somme parziali s N converge ad un limite finito S e Quindi possiamo dire che a N s N s N S S 0
4 6 Roberto Tauraso - Analisi Criterio di non convergenza Se a n 0 allora la serie a n non è convergente Vedremo nelle prossime sezioni che questa condizione è solo necessaria e non sufficiente ossia esistono esempi di serie che non convergono ma il cui termine generico è infinitesimo La serie geometrica La serie geometrica di ragione x R è la serie delle potenze intere di x: x n Per determinare il carattere di questo particolare tipo di serie dobbiamo studiarne le somme parziali N s N + x + + x N x n Se x allora s N N + e quindi per N la serie diverge a + Se x, notiamo che se moltiplichiamo s N per x otteniamo (x ) ( + x + + x N ) (x + + x N + x N+ ) ( + x + + x N ) e semplificando i termini opposti si ha che Quindi se x (x ) ( + x + + x N ) x N+ s N N x n xn+ x A questo punto il calcolo del limite per N diventa più semplice perché basta studiare il comportamento del termine x N+ Dato che lim N xn+ + se x > 0 se x < non esiste se x la risposta completa al problema della determinazione del carattere di una serie geometrica è la seguente
5 Serie numeriche e serie di potenze 7 Serie geometrica + se x x n se x < x non esiste se x Esempio La serie di cui abbiamo parlato nell introduzione è proprio la serie geometrica di ragione x con la sola differenza che in questo caso la somma parte dall indice e non da 0: ( ) n Dato che < la serie converge e per determinarne la somma basta osservare che n ( ) n n ( ) n ( ) 0 Dunque utilizzando la formula generale ritroviamo il risultato che avevamo dedotto con il ragionamento geometrico: Esempio A quale numero razionale corrisponde ? Dato che < allora 0 Quindi ) 0 ( ( ) n 0 0 ( ) n Esempio Calcolare ( ) n n+
6 8 Roberto Tauraso - Analisi Cerchiamo di ricondurre questa serie ad una serie geometrica notando che n+ 9 n : ( ) n ( n+ n 9) Il numero moltiplica ogni termine della serie e dunque può essere raccolto fuori dal segno di sommatoria: ( ) n ( n+ n 9) A questo punto la serie da determinare è la serie geometrica di ragione con l indice 9 n che parte da (e non da 0) Se si osserva che allora ( 9) n ( n ( 9) 0 ( 9) 9) ( ) n n+ ( ( ) ) n ( ) n + 9 9, Dato che < abbiamo che la serie converge e la sua somma vale: 9 ( ) n ( n ) 70 Esempio 4 Consideriamo un segmento di lunghezza (passo 0) e incolliamo al centro un triangolo equilatero di lato (passo ) Al passo successivo aggiungiamo al centro di ciascun lato (ora sono 4) un triangolo equilatero di lato (passo ) 9 passo 0 passo passo Continuando indefinitamente questo procedimento generiamo una figura geometrica dal bordo sempre più frastagliato Calcoliamo l area di questa figura Denotiamo con A N l area della figura al passo N così A 0 0, A 6, A
7 Serie numeriche e serie di potenze 9 Inoltre ad ogni passo successivo il numero di triangoli aggiunti aumenta, rispetto al passo precedente, di un fattore 4 mentre la loro area diminuisce di un fattore Ne 9 segue che A N ( ) 4 N 9 6 e al limite A Provate a verificare che al limite il perimetro tende a + 6 N ( ) n 4 9 Serie a termini non negativi Se i termini a n di una serie sono maggiori o uguali a zero allora lo studio del carattere della serie risulta essere in qualche modo piú semplice Notiamo infatti che la successione delle somme parziali in questo caso è crescente in quanto s N+ s N + a N s N e dunque, quando calcoliamo la somma della serie passando al limite, i possibili risultati sono solo due: la serie converge ad un numero non negativo oppure la serie diverge a + La semplice osservazione che le serie a termini non negativi non possono essere indeterminate ci permette di enunciare il primo criterio di convergenza Siano a n e Criterio del confronto b n due serie tali che 0 a n b n per n n 0 Allora () Se () Se b n converge allora anche a n + allora anche a n converge b n + Cerchiamo di applicare questo criterio per dimostrare che la serie armonica diverge n + n Per farlo scriviamo i primi termini della somma e raggruppiamoli opportunamente Poi costruiamo una nuova serie che minori la serie armonica sostituendo ogni termine di ciascun gruppo con un numero più piccolo:
8 0 Roberto Tauraso - Analisi ( + ) ( ) ( ) } {{ 4} } {{ 8} } {{ 6} + n n + + Quindi la serie minorante diverge e per il punto () del criterio del confronto anche la serie armonica diverge (anche se il suo termine generico è infinitesimo!) n Un altro ragionamento per confronto si può fare per determinare il carattere della serie armonica generalizzata n α dove α R L eventuale convergenza dipende dall esponente: α è il valore critico oltre il quale la serie converge: Serie armonica generalizzata n { converge se α > n α + se α Per verificare la divergenza nel caso α < basta semplicemente osservare che per n, n α n e quindi n n α Dunque, per il criterio del confronto, la divergenza di questa serie deriva dalla divergenza della serie armonica Per provare la convergenza nel caso α > si può ancora ricorrere al criterio del confronto Senza entrare in dettagli, qui ci limiteremo solo a dare un idea della dimostrazione attraverso un immagine geometrica α α α α + α + 4 α + 8 α + 7 α 6 α 5 α 4 α / α
9 Serie numeriche e serie di potenze I termini della serie armonica generalizzata corrispondono alle aree dei rettangoli ombreggiati Tali rettangoli vengono incasellati a gruppi di potenze di due all interno di un rettangolo di altezza e base uguale alla somma della serie geometrica di ragione / α Se α > allora / α < e la serie geometrica converge Possiamo così concludere che l area del rettangolo contenitore è finita e dunque è finita anche la somma infinita dei rettangoli contenuti Un problema ben più complicato è stabilire la somma della serie armonica generalizzata Per curiosità diamo la somma solo per α : n n π 6 Un risultato di convergenza più generale del precedente che ci capiterà di utilizzare è il seguente: Serie armonica generalizzata II n { converge se α > oppure se α e β > n α (log n) β + se α < oppure se α e β L analisi che abbiamo compiuto per queste serie è stata piuttosto faticosa, e per continuare con esempi più complicati abbiamo bisogno di altri criteri di convergenza che siano più facili da usare Cominciamo con il criterio del confronto asintotico Siano a n e Criterio del confronto asintotico b n due serie tali che a n 0, b n > 0 per n n 0 e a n lim L [0, + ] n b n Allora () Se L 0 e b n converge allora anche a n converge () Se L + e b n + allora anche a n + () Se 0 < L < + allora b n converge se e solo se a n converge Nel caso () le due serie si dicono asintoticamente equivalenti
10 Roberto Tauraso - Analisi Vediamone subito qualche applicazione Esempio Determinare il carattere della serie 7 n6 + n n 5 + n Dopo aver verificato che la serie è a termini non negativi proviamo a fare un analisi asintotica del termine generico ossia a determinare il suo ordine di infinitesimo 7 n6 + n n n n 7 5 n 9 n 9/7 Quindi la serie in esame è asintoticamente equivalente alla serie armonica con α 9 7 > che converge Dunque per il criterio del confronto asintotico anche la serie proposta converge Esempio Determinare il carattere della serie n n ( cos ( )) n La serie è a termini non negativi Ora facciamo l analisi asintotica del termine generico: ricordando che cos x x per x che tende a 0, si ha che n ( cos ( )) ( ) n n n 4 n Quindi la serie in esame è asintoticamente equivalente alla serie armonica con α che diverge Dunque per il criterio del confronto asintotico anche la serie proposta diverge Esempio Determinare il carattere della serie al variare del parametro reale a n log(n + )! log n! n log a (n + 6) La serie è a termini non negativi e l analisi asintotica del termine generico ci da: log(n + )! log n! n log a (n + 6) log((n + )!/n!) n log a (n + 6) log(n ) n(log n) a n(log n) a Quindi la serie in esame è asintoticamente equivalente alla serie armonica generalizzata con α e β a, dunque per il criterio del confronto asintotico la serie proposta converge se e solo se β > ossia se a > Vediamo altri due criteri di convergenza la cui dimostrazione è basata sul confronto con una serie geometrica
11 Serie numeriche e serie di potenze Sia Criterio del rapporto a n una serie tale che a n > 0 per n n 0 e Allora () Se L < allora () Se L > allora a n+ lim n a n a n converge b n + L [0, + ] Se L il criterio non dà una risposta e la serie potrebbe sia convergere che divergere Esempio 4 Determinare il carattere della serie Applichiamo il criterio del rapporto: a n+ n+ /(n + )! a n n /n! n n! Quindi il limite è minore di e la serie converge Esempio 5 Determinare il carattere della serie Applichiamo il criterio del rapporto: a n+ a n n+ n! n (n + )! n + 0 n n! n n (n + )! nn (n + ) nn n! (n + ) n+ (n + ) n n n+ Dato che <, la serie converge e (n + ) ( ) n + n e n
12 4 Roberto Tauraso - Analisi Sia Criterio della radice a n una serie tale che a n 0 per n n 0 e Allora () Se L < allora () Se L > allora lim n a n converge a n + n an L [0, + ] Se L il criterio non dà una risposta e la serie potrebbe sia convergere che divergere Esempio 6 Determinare il carattere della serie Applichiamo il criterio della radice: n n n n ( n ) /n n 0 Il limite è minore di e quindi la serie converge Notiamo che l applicazione del criterio del rapporto o della radice alla serie armonica generalizzata è inefficace perché in entrambi i casi il limite è qualunque sia il valore dell esponente α: /(n + ) α /n α ( ) α n e n + ( ) α n n n α n (si ricorda che n n ) Concludiamo con un esempio dove si utilizza una tecnica mista Esempio 7 Determinare il carattere della serie n n + 5 n n cos n Dopo aver osservato che la serie è a termini positivi (n > cos n per n ) facciamo un analisi asintotica n + 5 n n cos n 5n n
13 Serie numeriche e serie di potenze 5 Quindi studiare la serie data è equivalente a studiare la serie n 5 n n Questa diverge perchè applicando il criterio della radice troviamo che n 5 n n 5 ( n n) 5 > 4 Serie a termini di segno variabile Qui discuteremo due criteri che possono aiutare lo studio della convergenza quando i termini della serie non hanno segno costante Il primo prevede di studiare la serie a termini non negativi ottenuta prendendo i valori assoluti dei termini della serie data Criterio della convergenza assoluta Se a n converge allora anche a n converge Anche se non ne diamo una dimostrazione, possiamo dire che se avessimo la libertà di modificare a piacere il segno di ogni termine, la serie dei valori assoluti rappresenterebbe il caso peggiore per avere la convergenza: in questo caso infatti le somme crescono andando in un unica direzione mentre se i segni sono variabili le somme si possono compensare Esempio 4 Determinare il carattere della serie n sin n n log( + n n ) Il segno dei termini è variabile per la presenza di sin n (e la distribuzione dei segni è piuttosto irregolare ) La serie dei valori assoluti è inoltre per confronto 0 n sin n n log( + n n ), sin n n log( + n n ) n log( + n n ) n log(n n ) n log n La serie individuata dai termini converge (serie armonica generalizzata II con n log n α e β ), e quindi converge anche la serie dei valori assoluti Per il criterio appena enunciato anche la serie data converge
14 6 Roberto Tauraso - Analisi Se la serie non è assolutamente convergente allora la determinazione del carattere della serie può essere molto complicato Basti pensare che per queste serie modificare l ordine in cui vengono sommati i termini può influenzare la somma della serie stessa Comunque, nel caso in cui i segni siano esattamente alternati vale il seguente criterio Sia Criterio di Leibnitz ( ) n a n una serie tale che a n 0 per n n 0 e () a n tende a zero; () a n è decrescente ossia a n a n+ per n n 0 Allora la serie converge Vediamone la dimostrazione Dato che i termini a n sono decrescenti al crescere di n e vengono alternativamente sommati e sottratti, le somme parziali oscillano sull asse reale nel seguente modo s 0 a 0, s s 0 a, s s + a, s s a, l l 0 s s s s 0 In particolare si può facilmente osservare che le somme parziali di indice pari s N decrescono mentre quelle di indice dispari s N+ crescono s N s N (a N a N ) s N, s N+ s N + ( a N+ + a N ) s N Inoltre siccome s s N+ s N a N+ s N s 0 possiamo dire che la successione di indice pari s N tende ad un limite l 0 mentre la successione di indice dispari tende ad un limite l : s N+ l l 0 s N Per dimostrare che la serie converge basta verificare che questi due limiti l e l sono uguali Dalla relazione s N+ s N + a N+ passando al limite e ricordando che la successione a n è infinitesima si ottiene proprio che l l e il valore comune è proprio la somma della serie
15 Serie numeriche e serie di potenze 7 Esempio 4 Determinare il carattere della serie ( ) n+ n Se prendiamo la serie dei valori assoluti la serie diventa la serie armonica che è divergente Quindi il criterio della convergenza assoluta non ci dà alcuna informazione utile Se applichiamo invece il criterio di Leibnitz otteniamo facilmente la convergenza della serie data perché decresce e tende a 0 n In seguito vedremo che la somma di questa serie è uguale a log : n log 6 È sorprendente notare che se in questa serie cambiamo l ordine in cui i termini vengono sommati possiamo ottenere una serie che converge ad una somma diversa! Per esempio, si può dimostrare che questo fenomeno accade se si alternano due termini di indice dispari e uno di indice pari: log Esempio 4 Determinare il carattere della serie cos(nπ) n + n log n Intanto osserviamo che cos(nπ) ( ) n e poi verifichiamo se la serie converge assolutamente ( ) n n + n log n n + n log n n log n Per quanto detto questa serie diverge e dunque la serie data non converge assolutamente Dato che la serie è a segni alterni, proviamo allora ad applicare il criterio di Leibnitz: n + n log n decresce e tende a 0 e quindi la serie data converge 5 Serie di potenze Fino a questo momento abbiamo considerato serie numeriche ossia somme infinite di numeri reali, qui invece parleremo di uno degli esempi più importanti di serie di
16 8 Roberto Tauraso - Analisi funzioni: le serie di potenze In realtà ne abbiamo già incontrato un esempio ossia la serie geometrica di ragione x: x n In particolare abbiamo visto che se viene assegnato un certo numero x la serie corrispondente converge ad un numero finito solo se x < Questo risultato può essere riletto nel seguente modo: la serie in questione definisce una funzione della variabile x il cui dominio D è l insieme in cui la serie converge, ossia l intervallo aperto di centro 0 e raggio : D (, ) Le serie di potenze sono un estensione della serie geometrica: le potenze sono centrate in un generico punto x 0 R e la potenza n-esima viene moltiplicata per un coefficiente reale a n : a n (x x 0 ) n Anche in questo caso si pone innanzi tutto il problema della determinazione del dominio di questa nuova funzione Si verifica che il dominio è ancora un intervallo (centrato in x 0 ) di un certo raggio R (detto di convergenza) Il calcolo di tale raggio si può effettuare nel seguente modo Raggio di convergenza Data la serie di potenze a n (x x 0 ) n a n+ () Se lim L [0, + ] allora R /L n a n () Se lim n n a n L [0, + ] allora R /L La dimostrazione nel primo caso è una semplice applicazione del criterio del rapporto alla serie dei valori assoluti a n x x 0 n Infatti calcolando il limite per n che tende a del rapporto tra due termini successivi si ottiene a n+ x x 0 n+ a n+ x x a n x x 0 n 0 L x x 0 a n Quindi si ha la convergenza (assoluta) se L x x 0 <, ossia se x x 0 < L R (se L + si pone R 0, mentre se L 0 si pone R + ) La serie invece non converge se L x x 0 >, ossia se x x 0 > L R
17 Serie numeriche e serie di potenze 9 In modo simile applicando il criterio della radice si ottiene il secondo caso La determinazione del raggio di convergenza, come suggerisce la dimostrazione precedente, non dà alcuna informazione sul carattere della serie agli estremi del dominio quando x x 0 R (ossia quando L x x 0 ) Per dare una risposta in questi casi basterà studiare le serie numeriche corrispondenti sostituendo a x i valori x 0 + R e x 0 R Esempio 5 Consideriamo la serie n n n (x )n Calcoliamo il raggio di convergenza utilizzando per esempio la formula con il rapporto: a n+ lim n a n n n lim n (n + ) n+ quindi il raggio di convergenza è e il dominio di convergenza D contiene l intervallo aperto di centro x 0 e raggio R ossia l intervallo (, ) Vediamo che cosa succede negli estremi e : Se x allora x e la serie diventa n n n (x )n n n n ( )n che converge per il criterio di Leibnitz e quindi D Se x allora x e la serie diventa n n n (x )n n n n n n ( ) n n, che diverge a + e quindi D Il dominio di convergenza è D [, ) Esempio 5 Consideriamo la serie ( n + n ) x n n Calcoliamo il raggio di convergenza utilizzando la formula con la radice n-sima: lim n n n, n n + n lim n n 8 n + 9 n lim n n 9 n 9 quindi il raggio di convergenza è Il dominio di convergenza D, dunque, contiene 9 l intervallo aperto di centro x 0 0 e raggio R ossia l intervallo (, ) Vediamo cosa succede negli estremi e : 9 9
18 40 Roberto Tauraso - Analisi Se x 9 allora la serie diventa ( n + n ) n ( 9) n ( ) n 8 ( ) n 9 + che non converge perché il termine della serie non tende a 0 Allo stesso modo la serie non converge neanche per x 9 Dunque il dominio di convergenza è D ( 9, 9 ) In alcuni casi è possibile determinare, oltre al calcolo del dominio, anche la somma della serie Qui riassumiamo gli esempi più importanti di serie di potenze per le quali la somma è una funzione esplicita Come si può notare, in questi casi le serie corrispondono proprio agli sviluppi di Taylor della funzione rispetto ai loro centri Ciò significa che per queste funzioni lo sviluppo di Taylor non serve solo ad approssimare i valori della funzione vicino al centro, ma su tutto il dominio della serie n Principali serie di potenze x x n per x D (, ) e x log( + x) sin x cos x arctan x x n n! ( ) n n+ xn n ( ) n x n+ (n + )! ( ) n xn (n)! ( ) n xn+ n + per x D R per x D (, ] per x D R per x D R per x D [, ] Esempio 5 Calcoliamo la somma della serie n + 5n n! Dopo aver verificato la sua convergenza possiamo intanto separare la serie in due parti n(n + 5) (n ) + 6 n! (n )! (n )! + 6 (n )!
19 Serie numeriche e serie di potenze 4 La prima serie può essere riscritta così (n )! n! (questi due cicli sommano gli stessi numeri!) Analogamente la seconda serie diventa Quindi n + 5n n! (n )! n ( n! + 6 n n! n! ) ( n! 7 n Ora possiamo utilizzare la serie di potenze relativa a e x per x : ) 6 n! n + 5n n! 7e 6 Vale la pena notare che le considerazioni fatte per le serie di potenze reali si estendono anche nel campo complesso: il dominio della serie di potenze a n (z z 0 ) n è questa volta un disco in C centrato in z 0 e raggio R Si osservi che rispetto al caso reale l analisi della convergenza nei punti del bordo del dominio può diventare più complicata perché ci sono infiniti punti da esaminare Esempio 54 Calcoliamo la somma della serie n ( ) n i Dato che i/ / <, i/ sta nel dominio di convergenza della serie geometrica in questione La somma vale n ( ) n i i i i i 0
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
e l insieme delle soluzioni, dopo le analoghe riduzioni del caso n = 2, si scrive come
 Numeri complessi 9 Da questi esempi si può osservare che, facendo le successive potene di un numero complesso, i punti corrispondenti girano attorno all origine. Se inoltre > allora i punti si allontanano
Numeri complessi 9 Da questi esempi si può osservare che, facendo le successive potene di un numero complesso, i punti corrispondenti girano attorno all origine. Se inoltre > allora i punti si allontanano
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
SOMMARIO. 13.1 I radicali pag. 3. 13.2 I radicali aritmetici pag. 5. 13.3 Moltiplicazione e divisione fra radicali aritmetici pag.
 SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
7 - Esercitazione sulle derivate
 7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
FUNZIONI REALI DI VARIABILE REALE e CONTINUITA Roberto Argiolas
 FUNZIONI REALI DI VARIABILE REALE e CONTINUITA Roberto Argiolas.8.6.. - -.5.5 -. In questa dispensa ricordiamo la classificazione delle funzioni elementari e il dominio di esistenza delle stesse. Inoltre
FUNZIONI REALI DI VARIABILE REALE e CONTINUITA Roberto Argiolas.8.6.. - -.5.5 -. In questa dispensa ricordiamo la classificazione delle funzioni elementari e il dominio di esistenza delle stesse. Inoltre
Il simbolo. è è = = = In simboli: Sia un numero naturale diverso da zero, il radicale. Il radicale. esiste. esiste 0 Il radicale
 Radicali 1. Radice n-esima Terminologia Il simbolo è detto radicale. Il numero è detto radicando. Il numero è detto indice del radicale. Il numero è detto coefficiente del radicale. Definizione Sia un
Radicali 1. Radice n-esima Terminologia Il simbolo è detto radicale. Il numero è detto radicando. Il numero è detto indice del radicale. Il numero è detto coefficiente del radicale. Definizione Sia un
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
 1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Capitolo 5. Funzioni. Grafici.
 Capitolo 5 Funzioni. Grafici. Definizione: Una funzione f di una variabile reale,, è una corrispondenza che associa ad ogni numero reale appartenente ad un insieme D f R un unico numero reale, y R, denotato
Capitolo 5 Funzioni. Grafici. Definizione: Una funzione f di una variabile reale,, è una corrispondenza che associa ad ogni numero reale appartenente ad un insieme D f R un unico numero reale, y R, denotato
Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno
 Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
Rappresentazione di numeri Complemento al corso di Fondamenti di Informatica I corsi di laurea in ingegneria, settore dell informazione Università la Sapienza Consorzio Nettuno Un numero e un entità teorica,
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
2 Argomenti introduttivi e generali
 1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
LIMITI E CONFRONTO LOCALE Esercizi svolti. b) lim. d) lim. h) lim x x + 1 x. l) lim. b) lim x cos x. x 0 sin 2 3x cos x p) lim.
 LIMITI E CONFRONTO LOCALE Esercizi svolti. Calcolare i seguenti iti: a + 4 + b + 4 + 4 c 5 e ± g i + + sin 4 m sin o π q sin π + 4 + 7 d + 4 + + 5 4 + f 4 4 + 5 4 + 4 h + + l + + cos n sin cos p π π +
LIMITI E CONFRONTO LOCALE Esercizi svolti. Calcolare i seguenti iti: a + 4 + b + 4 + 4 c 5 e ± g i + + sin 4 m sin o π q sin π + 4 + 7 d + 4 + + 5 4 + f 4 4 + 5 4 + 4 h + + l + + cos n sin cos p π π +
Analisi Complessa. Prova intermedia del 7 novembre 2002 - Soluzioni. (z 11 1) 11 1 = 0.
 Analisi Complessa Prova intermedia del 7 novembre 2002 - Soluzioni Esercizio. Si consideri l equazione z 0. Quante soluzioni distinte esistono in C? Quante di esse sono contenute all interno del disco
Analisi Complessa Prova intermedia del 7 novembre 2002 - Soluzioni Esercizio. Si consideri l equazione z 0. Quante soluzioni distinte esistono in C? Quante di esse sono contenute all interno del disco
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : = y
 Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Numeri complessi. x 2 = 1.
 1 Numeri complessi Nel corso dello studio della matematica si assiste ad una progressiva estensione del concetto di numero. Dall insieme degli interi naturali N si passa a quello degli interi relativi
1 Numeri complessi Nel corso dello studio della matematica si assiste ad una progressiva estensione del concetto di numero. Dall insieme degli interi naturali N si passa a quello degli interi relativi
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Il principio di induzione e i numeri naturali.
 Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
LE FUNZIONI E LE LORO PROPRIETÀ
 LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
1 Principali funzioni e loro domini
 Principali funzioni e loro domini Tipo di funzione Rappresentazione Dominio Polinomio intero p() = a n + + a n R p() Polinomio fratto q() 6= q() 2n Radici pari p f() f() 2n+ Radici dispari p f() R Moduli
Principali funzioni e loro domini Tipo di funzione Rappresentazione Dominio Polinomio intero p() = a n + + a n R p() Polinomio fratto q() 6= q() 2n Radici pari p f() f() 2n+ Radici dispari p f() R Moduli
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
La f(x) dovrà rimanere all interno di questo intorno quando la x è all interno di un intorno di x 0, cioè I(x 0 ), cioè:
 1 Limiti Roberto Petroni, 2011 Possiamo introdurre intuitivamente il concetto di limite dicendo che quanto più la x si avvicina ad un dato valore x 0 tanto più la f(x) si avvicina ad un valore l detto
1 Limiti Roberto Petroni, 2011 Possiamo introdurre intuitivamente il concetto di limite dicendo che quanto più la x si avvicina ad un dato valore x 0 tanto più la f(x) si avvicina ad un valore l detto
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Le funzioni elementari. La struttura di R. Sottrazione e divisione
 Le funzioni elementari La struttura di R La struttura di R è definita dalle operazioni Addizione e moltiplicazione. Proprietà: Commutativa Associativa Distributiva dell addizione rispetto alla moltiplicazione
Le funzioni elementari La struttura di R La struttura di R è definita dalle operazioni Addizione e moltiplicazione. Proprietà: Commutativa Associativa Distributiva dell addizione rispetto alla moltiplicazione
La trasformata Zeta. Marco Marcon
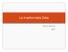 La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
La trasformata Zeta Marco Marcon ENS Trasformata zeta E l estensione nel caso discreto della trasformata di Laplace. Applicata all analisi dei sistemi LTI permette di scrivere in modo diretto la relazione
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
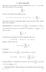 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
