4 FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMO
|
|
|
- Gerardina Pippi
- 8 anni fa
- Visualizzazioni
Transcript
1 4 FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMO 4.0. Esponenziale. Nella prima sezione abbiamo definito le potenze con esponente reale. Vediamo ora in dettaglio le proprietà della funzione esponenziale a, a > 0, R. Proprietà 4. (Proprietà dell esponenziale). Siano, z R e a > 0. Allora (i) a 0 = 0. (ii) a > 0 R. (iii) a +z = a a z R. (iv) Se a >, allora: a < a z < z. (vi) Se 0 < a <, allora: a > a z < z. (v) Se a >, allora: (vii) Se 0 < a <, allora: lim = a = 0 e lim =+ a = +. lim = a = + e lim =+ a = 0. Esempio 4.2 Grafico di f() = 2 e g() = ( 2) = 2 = f( ). g() = 2 f() = 2 La funzione f() = a, con a >, gode delle seguenti proprietà. f ha come dominio tutta la retta reale. Intersezioni con gli assi: punto di coordinate (0,). f() > 0 R. f è strettamente crescente su R. lim = a = 0 e lim =+ a = +. 38
2 La funzione f() = a, con 0 < a <, gode delle seguenti proprietà. f ha come dominio tutta la retta reale. Intersezioni con gli assi: punto di coordinate (0,). f() > 0 R. f è strettamente decrescente su R. lim =+ a = 0 e lim = a = +. Proprietà 4.3 (Altre proprietà delle potenze). Siano a, b > 0,, R. Allora (i) (a b) = a b. (ii) (a ) = a. (iii) a + = a a R. (iv) a < b a < b > 0 (v) a > b a < b < 0 Esempio 4.4 Il disegno sottostante illustra le proprietà (iv) e (v) con a = 2 e b = 3. f() = 2 g() = 3 Esercizio 4.5 Risolvere la disequazione: 3 >. Ricordiamo che = 3 0, quindi 3 > 3 > 3 0 > 0 < 0 39
3 4. Numero e di Nepero Definizione 4.6 Definiamo il numero e di Nepero mediante ( e = lim + n. n + n) Osserviamo che il limite nella definizione presenta la forma di indecisione. Inoltre l esistenza del limite è garantita dal fatto (non ovvio) che la successione n ( + n) n è monotona crescente e limitata, quindi il limite esiste ed è finito (si veda per esempio Bramanti, Pagani, Salsa, MATEMATICA Calcolo infinitesimale e algebra lineare, Zanichelli). il numero e di Nepero è irrazionale, ovvero ha infinite cifre dopo la virgola. Una prima approssimazione di e è la seguente: e = 2, Ricordiamo la definizione di k! con k intero non negativo. Abbiamo 0! = k! = k (k ) (k 2) (k 3) 3 2 Si dimostra che In particolare e = + k=0 e = + k=0 k k! R. k! = Questa espressione permette di calcolare valori approssimati di e. Esempio 4.7 Grafico di f() = e e g() = e. g() = e f() = e 40
4 4.2 Logaritmo. La funzione logaritmo è definita come la funzione inversa della funzione esponenziale. Più precisamente se a > 0 e a, allora il logaritmo in base a di > 0 è il numero reale dato da: = log a a =. In altre parole = log a è l esponente da dare alla base a per ottenere l argomento del logaritmo. Per esempio log 2 8 = 3, infatti 2 3 = 8. In generale dalla definizione segue log a a =. Proprietà 4.8 (Proprietà del logaritmo). Siano, z > 0, a > 0 e a. Allora (i) a log a = ; (ii) log a = 0; (iii) log a a = ; (iv) log a (z) = log a + log a z; (v) log a ( β ) = β log a ; (vi) log a z = log a log a z; (vii) log a = log a ; (viii) log a = log b log b a, b > 0 e b. Dimostrazione. (i) L uguaglianza a log a = segue direttamente dalla definizione; (ii) log a = a = = 0. (iii) log a a = a = a =. (iv) Dalla (i) otteniamo: log a (z) = log a +log a z z = a log a (z) = a log a +log a z = a log a a log a z = z. (v) Dalla (i) otteniamo: log a ( β ) = β log a a log a (β) = a β log a a log a (β) = ( a log a ) β ( β ) = () β ; (vi) Dalla (iv) e dalla (v) otteniamo: log a z = log a z = log a + log a z = log a log a z; (vii) Dalla (i) otteniamo: log a = log alog a = a log ( ) a a = a log a ( = ) log a a = ; (viii) Dalla (i) otteniamo: log a = log b log b a log b = log b a log a b log b = b log b a log a = ( b log b a) log a = a log a. 4
5 Esempio 4.9 Grafico di f() = log a e g() = log = f(). Nel disegno abbiamo preso a = 2. Come a osservato nella sottosezione??, il grafico di f() = log a è simmetrico al grafico di f () = a rispetto alla bisettrice di equazione =. f() = log a g() = log a Definizione 4.0 La funzione f() = ln = log e prende il nome di logaritmo naturale. La funzione f() = log a, con a > (quindi in particolare f() = ln), gode delle seguenti proprietà. Il dominio di f è la semiretta positiva (0, + ). Intersezioni con gli assi: punto di coordinate (,0). f() > 0 per > 0 e f() < 0 per 0 < <. f è strettamente crescente su R, ovvero: log a < log a z < z. lim 0 + log a = e lim + log a = +. La retta di equazione = 0 è un asintoto verticale. La funzione f() = log b, con 0 < b <, gode delle seguenti proprietà. Il dominio di f è la semiretta positiva (0, + ). Intersezioni con gli assi: punto di coordinate (,0). 42
6 f() > 0 per 0 < < e f() < 0 per > 0. f è strettamente decrescente su R, ovvero: log a < log a z > z. lim 0 + log a = + e lim + log a =. La retta di equazione = 0 è un asintoto verticale. Esempio 4. Risolvere la disequazione ln() > 3. Essendo 3 = ln(e 3 ) ed essendo f() = ln() una funzione strettamente crescente, otteniamo: ln() > 3 ln() > ln(e 3 ) ln() > ln(e 3 ) > e 3. Esempio 4.2 Risolvere la disequazione log 2 < 3. Essendo 3 = log 2(2 3) = log 2 ( 3 2 ) ed essendo f() = log 2 una funzione strettamente crescente, otteniamo: log 2 < 3 log 2 < log 2 ( 3 2 ) 0 < < 3 2. = log = 3 43
0 + = + 3 x lim 1 + (log 2 x)100 = 0
 (log a ) γ = 0, a, b > γ R. (log a ) γ = (log a ) γ a = +, a > β R. β a β = = β a 0 + = +. = 0 0 = 0 β = +, (log a ) γ a > β > 0, γ R. β (log a ) γ = (log a) γ = 0 + = +. β = +, a, b > γ R. (log a ) γ
(log a ) γ = 0, a, b > γ R. (log a ) γ = (log a ) γ a = +, a > β R. β a β = = β a 0 + = +. = 0 0 = 0 β = +, (log a ) γ a > β > 0, γ R. β (log a ) γ = (log a) γ = 0 + = +. β = +, a, b > γ R. (log a ) γ
FUNZIONI ESPONENZIALE E LOGARITMICA
 FUNZIONI ESPONENZIALE E LOGARITMICA Le potenze con esponente reale La potenza a x di un numero reale a è definita se a>0 per ogni x R se a=0 per tutti e soli i numeri reali positivi ( x R + ) se a
FUNZIONI ESPONENZIALE E LOGARITMICA Le potenze con esponente reale La potenza a x di un numero reale a è definita se a>0 per ogni x R se a=0 per tutti e soli i numeri reali positivi ( x R + ) se a
0 < a < 1 a > 1. In entrambi i casi la funzione y = log a (x) si può studiare per punti e constatare che essa presenta i seguenti andamenti y
 INTRODUZIONE Osserviamo, in primo luogo, che le funzioni logaritmiche sono della forma y = log a () con a costante positiva diversa da (il caso a = è banale per cui non sarà oggetto del nostro studio).
INTRODUZIONE Osserviamo, in primo luogo, che le funzioni logaritmiche sono della forma y = log a () con a costante positiva diversa da (il caso a = è banale per cui non sarà oggetto del nostro studio).
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : = y
 Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
Funzioni inverse Simmetrie rispetto alla bisettrice dei quadranti dispari. Consideriamo la trasformazione descritta dalle equazioni : ' = y y' = Consideriamo il punto P(,5) se eseguiamo tra trasformazione
SOLUZIONI D = (-1,+ ).
 SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
SOLUZIONI. Data la funzione f() ( ) ln( ) a) trova il dominio di f b) indica quali sono gli intervalli in cui f() risulta positiva e quelli in cui risulta negativa c) determina le eventuali intersezioni
Capitolo 5. Funzioni. Grafici.
 Capitolo 5 Funzioni. Grafici. Definizione: Una funzione f di una variabile reale,, è una corrispondenza che associa ad ogni numero reale appartenente ad un insieme D f R un unico numero reale, y R, denotato
Capitolo 5 Funzioni. Grafici. Definizione: Una funzione f di una variabile reale,, è una corrispondenza che associa ad ogni numero reale appartenente ad un insieme D f R un unico numero reale, y R, denotato
Funzione logaritmo con. funzione inversa della funzione di
 FUNZIONE LOGARITMO a è la base della funzione logaritmo ed è una costante positiva fissata e diversa da 1 x è l argomento della funzione logaritmo e varia nel dominio Funzione logaritmo con funzione inversa
FUNZIONE LOGARITMO a è la base della funzione logaritmo ed è una costante positiva fissata e diversa da 1 x è l argomento della funzione logaritmo e varia nel dominio Funzione logaritmo con funzione inversa
ISTITUTO ISTRUZIONE SUPERIORE "L. EINAUDI" ALBA ANNO SCOLASTICO 2014/2015
 ISTITUTO ISTRUZIONE SUPERIORE "L. EINAUDI" ALBA ANNO SCOLASTICO 2014/2015 CLASSE 4^ B SETTORE TECNOLOGICO: Costruzioni, Ambiente e Territorio Disciplina: Matematica Testi in uso: Nuova Matematica a Colori-3
ISTITUTO ISTRUZIONE SUPERIORE "L. EINAUDI" ALBA ANNO SCOLASTICO 2014/2015 CLASSE 4^ B SETTORE TECNOLOGICO: Costruzioni, Ambiente e Territorio Disciplina: Matematica Testi in uso: Nuova Matematica a Colori-3
Esponenziali e logaritmi
 Esponenziali e logaritmi Corso di accompagnamento in matematica Lezione 4 Sommario 1 La funzione esponenziale Proprietà Grafico 2 La funzione logaritmo Grafico Proprietà 3 Equazioni / disequazioni esponenziali
Esponenziali e logaritmi Corso di accompagnamento in matematica Lezione 4 Sommario 1 La funzione esponenziale Proprietà Grafico 2 La funzione logaritmo Grafico Proprietà 3 Equazioni / disequazioni esponenziali
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Chi non risolve esercizi non impara la matematica.
 .6 esercizi 3 Esercizio 8. Stabilisci se la funzione = 4 è pari o dispari. Soluzione. Sostituiamo al posto di in f(): f( ) = ( ) 4 ( ) = 4 = f() La funzione è pari. Vedi le figure 4f e 30f..6 esercizi
.6 esercizi 3 Esercizio 8. Stabilisci se la funzione = 4 è pari o dispari. Soluzione. Sostituiamo al posto di in f(): f( ) = ( ) 4 ( ) = 4 = f() La funzione è pari. Vedi le figure 4f e 30f..6 esercizi
Anno 5 4 Funzioni reali. elementari
 Anno 5 4 Funzioni reali elementari 1 Introduzione In questa lezione studieremo alcune funzioni molto comuni, dette per questo funzioni elementari. Al termine di questa lezione sarai in grado di definire
Anno 5 4 Funzioni reali elementari 1 Introduzione In questa lezione studieremo alcune funzioni molto comuni, dette per questo funzioni elementari. Al termine di questa lezione sarai in grado di definire
I tre concetti si possono descrivere in modo unitario dicendo che f e iniettiva, suriettiva, biiettiva se e solo se per ogni b B l equazione
 Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
PROGRAMMAZIONE COORDINATA TEMPORALMENTE A.S. 2014/2015 - CLASSI: 4AMM-4BME
 DIPARTIMENTO: PROGRAMMAZIONE COORDINATA TEMPORALMENTE A.S. 2014/2015 - : 4AMM-4BME E Monte ore annuo 132 (99+33) Libro di Testo L. Sasso: Nuova Matematica a colori Edizione Verde, VOL.3-4 SETTEMBRE OTTOBRE
DIPARTIMENTO: PROGRAMMAZIONE COORDINATA TEMPORALMENTE A.S. 2014/2015 - : 4AMM-4BME E Monte ore annuo 132 (99+33) Libro di Testo L. Sasso: Nuova Matematica a colori Edizione Verde, VOL.3-4 SETTEMBRE OTTOBRE
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Esponenziali e logaritmi
 Istituto d Istruzione Superiore A Tilgher Ercolano (Na) Prof Amendola Alfonso Premessa Esponenziali e logaritmi Questa breve trattazione non vuole costituire una guida completa ed esauriente sull argomento,
Istituto d Istruzione Superiore A Tilgher Ercolano (Na) Prof Amendola Alfonso Premessa Esponenziali e logaritmi Questa breve trattazione non vuole costituire una guida completa ed esauriente sull argomento,
FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMICA
 FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMICA DEFINIZIONE: Dato un numero reale a che sia a > 0 e a si definisce funzione esponenziale f(x) = a x la relazione che ad ogni valore di x associa uno e un solo
FUNZIONE ESPONENZIALE E FUNZIONE LOGARITMICA DEFINIZIONE: Dato un numero reale a che sia a > 0 e a si definisce funzione esponenziale f(x) = a x la relazione che ad ogni valore di x associa uno e un solo
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
x ( 3) + Inoltre (essendo il grado del numeratore maggiore del grado del denominatore, d ancora dallo studio del segno),
 6 - Grafici di funzioni Soluzioni Esercizio. Studiare il grafico della funzione f(x) = x x + 3. ) La funzione è definita per x 3. ) La funzione non è né pari, né dispari, né periodica. 3) La funzione è
6 - Grafici di funzioni Soluzioni Esercizio. Studiare il grafico della funzione f(x) = x x + 3. ) La funzione è definita per x 3. ) La funzione non è né pari, né dispari, né periodica. 3) La funzione è
ISTITUTO TECNICO INDUSTRIALE STATALE "G
 DIPARTIMENTO: ANNO SCOLASTICO 2014/2015 PROGRAMMAZIONE COORDINATA TEMPORALMENTE CLASSE: 4 AII-ABIT - pag. 1 PROGRAMMAZIONE COORDINATA TEMPORALMENTE A.S. 2014/2015 - CLASSE: 4AII-4BIT CLASSE E Monte ore
DIPARTIMENTO: ANNO SCOLASTICO 2014/2015 PROGRAMMAZIONE COORDINATA TEMPORALMENTE CLASSE: 4 AII-ABIT - pag. 1 PROGRAMMAZIONE COORDINATA TEMPORALMENTE A.S. 2014/2015 - CLASSE: 4AII-4BIT CLASSE E Monte ore
Determinare il dominio e la derivata delle seguenti funzioni e studiarne la monotonia ed eventuali massimi/minimi. ( ) x + 2.
 Determinare il dominio e la derivata delle seguenti funzioni e studiarne la monotonia ed eventuali massimi/minimi (1) (2) (3) (4) f (x) = log ( ) x + 2 x 1 f (x) = x exp( x 3 ) ( f (x) = arctan x ) x 1
Determinare il dominio e la derivata delle seguenti funzioni e studiarne la monotonia ed eventuali massimi/minimi (1) (2) (3) (4) f (x) = log ( ) x + 2 x 1 f (x) = x exp( x 3 ) ( f (x) = arctan x ) x 1
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
FUNZIONI ELEMENTARI Esercizi risolti
 FUNZIONI ELEMENTARI Esercizi risolti 1 Discutendo graficamente la disequazione x > 3+x, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi Rappresentare nel piano x, y) l insieme
FUNZIONI ELEMENTARI Esercizi risolti 1 Discutendo graficamente la disequazione x > 3+x, verificare che l insieme delle soluzioni è un intervallo e trovarne gli estremi Rappresentare nel piano x, y) l insieme
1 Limiti e continuità per funzioni di una variabile
 1 Limiti e continuità per funzioni di una variabile Considerazioni introduttive Consideriamo la funzione f() = sin il cui dominio naturale è
1 Limiti e continuità per funzioni di una variabile Considerazioni introduttive Consideriamo la funzione f() = sin il cui dominio naturale è
Le funzioni elementari. Corsi di Laurea in Tecniche di Radiologia... A.A. 2010-2011 - Analisi Matematica - Le funzioni elementari - p.
 Le funzioni elementari Corsi di Laurea in Tecniche di Radiologia... A.A. 200-20 - Analisi Matematica - Le funzioni elementari - p. /43 Funzioni lineari e affini Potenze ad esponente naturale Confronto
Le funzioni elementari Corsi di Laurea in Tecniche di Radiologia... A.A. 200-20 - Analisi Matematica - Le funzioni elementari - p. /43 Funzioni lineari e affini Potenze ad esponente naturale Confronto
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Coordinate Cartesiane nel Piano
 Coordinate Cartesiane nel Piano O = (0,0) origine degli assi ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi, y sistemi dimetrici: unità di misura diverse sui due assi (spesso
Coordinate Cartesiane nel Piano O = (0,0) origine degli assi ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi, y sistemi dimetrici: unità di misura diverse sui due assi (spesso
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
 1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
Esercizi sullo studio completo di una funzione
 Esercizi sullo studio completo di una funzione. Disegnare il grafico delle funzioni date, utilizzando ogni informazione utile che si può ricavare dalla funzione e dalle sue derivate prima e seconda. a.
Esercizi sullo studio completo di una funzione. Disegnare il grafico delle funzioni date, utilizzando ogni informazione utile che si può ricavare dalla funzione e dalle sue derivate prima e seconda. a.
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Funzione reale di variabile reale
 Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Laurea in Scienze e Tecnologie Agrarie Corso Integrato: Matematica e Statistica Modulo: Matematica (6 CFU) (4 CFU Lezioni +2 CFU Esercitazioni) Corso di Laurea in Tutela e Gestione del territorio
Corso di Laurea in Scienze e Tecnologie Agrarie Corso Integrato: Matematica e Statistica Modulo: Matematica (6 CFU) (4 CFU Lezioni +2 CFU Esercitazioni) Corso di Laurea in Tutela e Gestione del territorio
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
FUNZIONI / ESERCIZI SVOLTI
 ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
SEGNO DELLA FUNZIONE. Anche in questo caso, per lo studio del segno della funzione, occorre risolvere la disequazione: y > 0 Ne segue:
 CAMPO DI ESISTENZA. Poiché la funzione data è una razionale fratta, essa risulta definita su tutto l asse reale tranne che nei punti in cui il denominatore della frazione si annulla, cioè: C.E. { R: 0}
CAMPO DI ESISTENZA. Poiché la funzione data è una razionale fratta, essa risulta definita su tutto l asse reale tranne che nei punti in cui il denominatore della frazione si annulla, cioè: C.E. { R: 0}
Funzione Una relazione fra due insiemi A e B è una funzione se a ogni elemento di A si associa uno e un solo elemento
 TERIA CAPITL 9. ESPNENZIALI E LGARITMI. LE FUNZINI Non si ha una funzione se anche a un solo elemento di A non è associato un elemento di B, oppure ne sono associati più di uno. DEFINIZINE Funzione Una
TERIA CAPITL 9. ESPNENZIALI E LGARITMI. LE FUNZINI Non si ha una funzione se anche a un solo elemento di A non è associato un elemento di B, oppure ne sono associati più di uno. DEFINIZINE Funzione Una
Il valore assoluto. F. Battelli Università Politecnica delle Marche, Ancona. Pesaro, Precorso di Analisi 1, 22-28 Settembre 2005 p.
 Il valore assoluto F Battelli Università Politecnica delle Marche Ancona Pesaro Precorso di Analisi 1 22-28 Settembre 2005 p1/23 Il valore assoluto Si definisce il valore assoluto di un numero reale l
Il valore assoluto F Battelli Università Politecnica delle Marche Ancona Pesaro Precorso di Analisi 1 22-28 Settembre 2005 p1/23 Il valore assoluto Si definisce il valore assoluto di un numero reale l
CLASSE terza SEZIONE E A.S. 2014-15 PROGRAMMA SVOLTO
 CLASSE terza SEZIONE E A.S. 2014-15 L insieme dei numeri razionali. Equazioni e disequazioni di primo grado Sistemi di equazioni e disequazioni di primo grado.. IL PIANO CARTESIANO Il piano cartesiano.
CLASSE terza SEZIONE E A.S. 2014-15 L insieme dei numeri razionali. Equazioni e disequazioni di primo grado Sistemi di equazioni e disequazioni di primo grado.. IL PIANO CARTESIANO Il piano cartesiano.
Le funzioni elementari. La struttura di R. Sottrazione e divisione
 Le funzioni elementari La struttura di R La struttura di R è definita dalle operazioni Addizione e moltiplicazione. Proprietà: Commutativa Associativa Distributiva dell addizione rispetto alla moltiplicazione
Le funzioni elementari La struttura di R La struttura di R è definita dalle operazioni Addizione e moltiplicazione. Proprietà: Commutativa Associativa Distributiva dell addizione rispetto alla moltiplicazione
Studio di una funzione. Schema esemplificativo
 Studio di una funzione Schema esemplificativo Generalità Studiare una funzione significa determinarne le proprietà ovvero Il dominio. Il segno. Gli intervalli in cui cresce o decresce. Minimi e massimi
Studio di una funzione Schema esemplificativo Generalità Studiare una funzione significa determinarne le proprietà ovvero Il dominio. Il segno. Gli intervalli in cui cresce o decresce. Minimi e massimi
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Soluzione Punto 1 Si calcoli in funzione di x la differenza d(x) fra il volume del cono avente altezza AP e base il
 Matematica per la nuova maturità scientifica A. Bernardo M. Pedone 74 PROBLEMA Considerata una sfera di diametro AB, lungo, per un punto P di tale diametro si conduca il piano α perpendicolare ad esso
Matematica per la nuova maturità scientifica A. Bernardo M. Pedone 74 PROBLEMA Considerata una sfera di diametro AB, lungo, per un punto P di tale diametro si conduca il piano α perpendicolare ad esso
LE FUNZIONI E LE LORO PROPRIETÀ
 LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
1 Appunti a cura di prof.ssa MINA Maria Letizia integrati e pubblicati in data 12/10/10
 FUNZIONE OMOGRAFICA ASINTOTO VERTICALE: ASINTOTO ORIZZONTALE: 1 abbiamo verificato che, applicando all iperbole equilatera base, la dilatazione verticale di coefficiente 7 e la traslazione di vettore di
FUNZIONE OMOGRAFICA ASINTOTO VERTICALE: ASINTOTO ORIZZONTALE: 1 abbiamo verificato che, applicando all iperbole equilatera base, la dilatazione verticale di coefficiente 7 e la traslazione di vettore di
PROVA N 1. 1. Elencare gli elementi che conviene esaminare per tracciare il grafico di una funzione y=f(x) PROVA N 2. è monotona in R?
 PROVA N 1 1. Elencare gli elementi che conviene esaminare per tracciare il grafico di una funzione y=f(). Studiare la funzione f()= 8+ 7 9 (Sono esclusi i flessi) 3. Data la funzione f()= 1 6 3 - +5-6
PROVA N 1 1. Elencare gli elementi che conviene esaminare per tracciare il grafico di una funzione y=f(). Studiare la funzione f()= 8+ 7 9 (Sono esclusi i flessi) 3. Data la funzione f()= 1 6 3 - +5-6
COGNOME... NOME... Classe... Data... 1.a Calcolare le seguenti espressioni: 3. 220 245
 Capitolo I radicali Risoluzione algebrica erifica per la classe seconda Espressioni numeriche Equazioni lineari Esistenza Operazioni Espressioni letterali.a Calcolare le seguenti espressioni:. 5. 8 3.
Capitolo I radicali Risoluzione algebrica erifica per la classe seconda Espressioni numeriche Equazioni lineari Esistenza Operazioni Espressioni letterali.a Calcolare le seguenti espressioni:. 5. 8 3.
a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:
![a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha: a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:](/thumbs/28/12902483.jpg) ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
PIANO DI LAVORO DEL PROFESSORE
 ISTITUTO DI ISTRUZIONE SUPERIORE STATALE IRIS VERSARI - Cesano Maderno (MB) PIANO DI LAVORO DEL PROFESSORE Indirizzo: LICEO SCIENTIFICO MATERIA: MATEMATICA ANNO SCOLASTICO: 2014-2015 PROF: MASSIMO BANFI
ISTITUTO DI ISTRUZIONE SUPERIORE STATALE IRIS VERSARI - Cesano Maderno (MB) PIANO DI LAVORO DEL PROFESSORE Indirizzo: LICEO SCIENTIFICO MATERIA: MATEMATICA ANNO SCOLASTICO: 2014-2015 PROF: MASSIMO BANFI
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
Note di matematica per microeconomia
 Note di matematica per microeconomia Luigi Balletta Funzioni di una variabile (richiami) Una funzione di variabile reale ha come insieme di partenza un sottoinsieme di R e come insieme di arrivo un sottoinsieme
Note di matematica per microeconomia Luigi Balletta Funzioni di una variabile (richiami) Una funzione di variabile reale ha come insieme di partenza un sottoinsieme di R e come insieme di arrivo un sottoinsieme
TEMATICA 1 - FUNZIONI ED EQUAZIONI
 Docente Materia Classe Cristina Frescura Matematica 4B Programmazione Preventiva Anno Scolastico 2012-2013 Data 28 novembre 2012 Obiettivi Cognitivi Nota bene: gli obiettivi minimi sono sottolineati U.D.
Docente Materia Classe Cristina Frescura Matematica 4B Programmazione Preventiva Anno Scolastico 2012-2013 Data 28 novembre 2012 Obiettivi Cognitivi Nota bene: gli obiettivi minimi sono sottolineati U.D.
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Disciplina: MATEMATICA e COMPLEMENTI di MATEMATICA - ore settimanali 3 Docente prof. Domenico QUARANTA. Quadro sintetico dei Moduli
 Classe 5S Sede di Alberobello A.S. 2015/2016 Indirizzo di studio Art. Produzione e Trasformazione Disciplina: MATEMATICA e COMPLEMENTI di MATEMATICA - ore settimanali 3 Docente prof. Domenico QUARANTA
Classe 5S Sede di Alberobello A.S. 2015/2016 Indirizzo di studio Art. Produzione e Trasformazione Disciplina: MATEMATICA e COMPLEMENTI di MATEMATICA - ore settimanali 3 Docente prof. Domenico QUARANTA
Svolgimento di alcuni esercizi del libro Matematica di Angelo Guerraggio
 Svolgimento di alcuni esercizi del libro Matematica di Angelo Guerraggio. Funzioni e insiemi numerici.4 Verificare che (A B) (A B) = (A A ) B. ) Sia (a, b) (A B) (A B). Allora a (A A ) e b B, da cui (a,
Svolgimento di alcuni esercizi del libro Matematica di Angelo Guerraggio. Funzioni e insiemi numerici.4 Verificare che (A B) (A B) = (A A ) B. ) Sia (a, b) (A B) (A B). Allora a (A A ) e b B, da cui (a,
Grafico qualitativo di una funzione reale di variabile reale
 Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
Grafico qualitativo di una funzione reale di variabile reale Mauro Saita 1 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Dicembre 2014 Indice 1 Qualè il grafico
Generalità sulle funzioni
 Capitolo Concetto di funzione Generalità sulle funzioni Definizione di funzione Definizione Dato un sottoinsieme non vuoto D di R, si chiama funzione reale di variabile reale, una relazione che ad ogni
Capitolo Concetto di funzione Generalità sulle funzioni Definizione di funzione Definizione Dato un sottoinsieme non vuoto D di R, si chiama funzione reale di variabile reale, una relazione che ad ogni
7 - Esercitazione sulle derivate
 7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
3. Quale affermazione è falsa?
 1. Quale affermazione è falsa? Se la funzione f) è continua e monotona crescente su R e se f) = 1 e f4) =, allora ha un unico zero nell intervallo, 4) f) non si annulla mai in R f ) > nell intervallo,
1. Quale affermazione è falsa? Se la funzione f) è continua e monotona crescente su R e se f) = 1 e f4) =, allora ha un unico zero nell intervallo, 4) f) non si annulla mai in R f ) > nell intervallo,
Ing. Alessandro Pochì
 Lo studio di unzione Ing. Alessandro Pochì Appunti di analisi Matematica per la Classe VD (a.s. 011/01) Schema generale per lo studio di una unzione Premessa Per Studio unzione si intende, generalmente,
Lo studio di unzione Ing. Alessandro Pochì Appunti di analisi Matematica per la Classe VD (a.s. 011/01) Schema generale per lo studio di una unzione Premessa Per Studio unzione si intende, generalmente,
Guida pratica per la prova scritta di matematica della maturità scientifica
 Giulio Donato Broccoli Guida pratica per la prova scritta di matematica della maturità scientifica Comprende: Metodi matematici fondamentali per affrontare i temi assegnati Esercizi interamente svolti
Giulio Donato Broccoli Guida pratica per la prova scritta di matematica della maturità scientifica Comprende: Metodi matematici fondamentali per affrontare i temi assegnati Esercizi interamente svolti
Corso di Analisi Matematica. Funzioni reali di variabile reale
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni reali di variabile reale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni reali di variabile reale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida. 4 x
 UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida Con questa guida si vuol proporre un esempio di studio di funzione con Derive. La versione che ho utilizzato per questo studio è la 6.0. Consideriamo
UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida Con questa guida si vuol proporre un esempio di studio di funzione con Derive. La versione che ho utilizzato per questo studio è la 6.0. Consideriamo
Stampa Preventivo. A.S. 2009-2010 Pagina 1 di 8
 Stampa Preventivo A.S. 2009-2010 Pagina 1 di 8 Insegnante MARINO CRISTINA Classe 5AT Materia matematica preventivo consuntivo 99 0 titolo modulo 51 RIPASSO 52 FUNZIONI REALI DI VARIABILE 53 CALCOLO INFINITESIMALE
Stampa Preventivo A.S. 2009-2010 Pagina 1 di 8 Insegnante MARINO CRISTINA Classe 5AT Materia matematica preventivo consuntivo 99 0 titolo modulo 51 RIPASSO 52 FUNZIONI REALI DI VARIABILE 53 CALCOLO INFINITESIMALE
VERIFICA DI MATEMATICA. CLASSI TERZE (3AS, 3BS, 3CS, 3DS, 3ES) 2 settembre 2013 COGNOME E NOME.. CLASSE.
 VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
RDefinizione (Funzione) . y. . x CAPITOLO 2
 CAPITOLO 2 Funzioni reali di variabile reale Nel capitolo precedente è stata introdotta la nozione generale di funzione f : A B, con A e B insiemi arbitrari. Nel presente capitolo si analizzeranno più
CAPITOLO 2 Funzioni reali di variabile reale Nel capitolo precedente è stata introdotta la nozione generale di funzione f : A B, con A e B insiemi arbitrari. Nel presente capitolo si analizzeranno più
Verica di Matematica su dominio e segno di una funzione [COMPITO 1]
![Verica di Matematica su dominio e segno di una funzione [COMPITO 1] Verica di Matematica su dominio e segno di una funzione [COMPITO 1]](/thumbs/20/454730.jpg) Verica di Matematica su dominio e segno di una funzione [COMPITO 1] Esercizio 1. Determinare il dominio delle seguenti funzioni: 1. y = 16 x ;. y = e 1 x +4 + x + x + 1; 3. y = 10 x x 3 4x +3x; 4. y =
Verica di Matematica su dominio e segno di una funzione [COMPITO 1] Esercizio 1. Determinare il dominio delle seguenti funzioni: 1. y = 16 x ;. y = e 1 x +4 + x + x + 1; 3. y = 10 x x 3 4x +3x; 4. y =
Quale delle funzioni elencate ha il grafico in figura? 1) f(x)=x 3-2 2) f(x)= x 3-2x 2 -(x-2) 3) f(x)= x 3-2x 2 + x-2 4) f(x)= x 4 -x 2-2
 Quale delle funzioni elencate ha il grafico in figura? 1) f(x)=x 3-2 2) f(x)= x 3-2x 2 -(x-2) 3) f(x)= x 3-2x 2 + x-2 4) f(x)= x 4 -x 2-2 SOLUZIONE: Si esclude subito la funzione 2) perché per x=0 vale
Quale delle funzioni elencate ha il grafico in figura? 1) f(x)=x 3-2 2) f(x)= x 3-2x 2 -(x-2) 3) f(x)= x 3-2x 2 + x-2 4) f(x)= x 4 -x 2-2 SOLUZIONE: Si esclude subito la funzione 2) perché per x=0 vale
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
1.2 Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche
 . Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
. Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
MATEMATICA TRIENNIO CORSO TURISTICO, AMMINISTRAZIONE FINANZA MARKETING, SISTEMI INFORMATIVI AZIENDALI
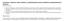 MATEMATICA TRIENNIO CORSO TURISTICO, AMMINISTRAZIONE FINANZA MARKETING, SISTEMI INFORMATIVI AZIENDALI Obiettivi del triennio: ; elaborando opportune soluzioni; 3) utilizzare le reti e gli strumenti informatici
MATEMATICA TRIENNIO CORSO TURISTICO, AMMINISTRAZIONE FINANZA MARKETING, SISTEMI INFORMATIVI AZIENDALI Obiettivi del triennio: ; elaborando opportune soluzioni; 3) utilizzare le reti e gli strumenti informatici
Calcolo differenziale Test di autovalutazione
 Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Funzioni esponenziali e logaritmiche. Mauro Saita. e-mail maurosaita@tiscalinet.it Versione provvisoria. Febbraio 2014
 Funzioni esponenziali e logaritmiche. Mauro Saita. e-mail maurosaita@tiscalinet.it Versione provvisoria. Febbraio 2014 Indice 1 Esponenziali 1 1.1 Funzioni esponenziali con dominio Z.......................
Funzioni esponenziali e logaritmiche. Mauro Saita. e-mail maurosaita@tiscalinet.it Versione provvisoria. Febbraio 2014 Indice 1 Esponenziali 1 1.1 Funzioni esponenziali con dominio Z.......................
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
FUNZIONI CONVESSE. + e x 0
 FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Matematica di base. Lezioni in Aula D5 ogni Venerdi alle 14:30 BLOG: matematicadibase.wordpress.com
 Matematica di base Lezioni in Aula D5 ogni Venerdi alle 14:30 BLOG: matematicadibase.wordpress.com Calendario 21 Ottobre Aritmetica ed algebra elementare 28 Ottobre Geometria elementare 4 Novembre Insiemi
Matematica di base Lezioni in Aula D5 ogni Venerdi alle 14:30 BLOG: matematicadibase.wordpress.com Calendario 21 Ottobre Aritmetica ed algebra elementare 28 Ottobre Geometria elementare 4 Novembre Insiemi
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Elementi di topologia della retta
 Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Esercizi di Matematica. Funzioni e loro proprietà
 www.pappalardovincenzo.3.it Esercizi di Matematica Funzioni e loro proprietà www.pappalardovincenzo.3.it ESERCIZIO www.pappalardovincenzo.3.it ESERCIZIO ESERCIZIO www.pappalardovincenzo.3.it ESERCIZIO
www.pappalardovincenzo.3.it Esercizi di Matematica Funzioni e loro proprietà www.pappalardovincenzo.3.it ESERCIZIO www.pappalardovincenzo.3.it ESERCIZIO ESERCIZIO www.pappalardovincenzo.3.it ESERCIZIO
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 2006/2007 SIMULAZIONE DI II PROVA - A
 LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
Docente: DI LISCIA F. CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI
 Docente: DI LISCIA F. Materia: MATEMATICA CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI Insiemi numerici: numeri naturali, proprietà delle operazioni aritmetiche; Potenze e loro proprietà; Criteri di divisibilità;
Docente: DI LISCIA F. Materia: MATEMATICA CLASSE 1T MODULO 1: GLI INSIEMI NUMERICI Insiemi numerici: numeri naturali, proprietà delle operazioni aritmetiche; Potenze e loro proprietà; Criteri di divisibilità;
11. Le funzioni composte
 . Le funzioni composte Definizione Date le due funzioni f A B e g D C, dove f[ A] D, si dice funzione composta di f e g la funzione h A C che ad ogni elemento a Afa corrispondere l elemento g(()) f a Ce
. Le funzioni composte Definizione Date le due funzioni f A B e g D C, dove f[ A] D, si dice funzione composta di f e g la funzione h A C che ad ogni elemento a Afa corrispondere l elemento g(()) f a Ce
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
PIANO DI LAVORO ANNUALE
 PIANO DI LAVORO ANNUALE ISTITUTO TECNICO ECONOMICO: INSEGNANTE: Consiglia Mazzone MATERIA DI INSEGNAMENTO: Matematica Applicata CLASSE IV sezione ITE Anno Scolastico 2014/2015 PARTE 1 LIVELLO COMPETENZE
PIANO DI LAVORO ANNUALE ISTITUTO TECNICO ECONOMICO: INSEGNANTE: Consiglia Mazzone MATERIA DI INSEGNAMENTO: Matematica Applicata CLASSE IV sezione ITE Anno Scolastico 2014/2015 PARTE 1 LIVELLO COMPETENZE
Programmi a.s. 2014-15
 Docente BARO MAVIS Classi 4 ENOGASTRONOMIA sezione/i Ce 1. Disequazioni e loro applicazione: Le disequazioni e le loro proprietà; Le disequazioni di primo e secondo grado; Le disequazioni di grado superiore
Docente BARO MAVIS Classi 4 ENOGASTRONOMIA sezione/i Ce 1. Disequazioni e loro applicazione: Le disequazioni e le loro proprietà; Le disequazioni di primo e secondo grado; Le disequazioni di grado superiore
Corso di Analisi Matematica. Funzioni continue
 a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Studio grafico-analitico delle funzioni reali a variabile reale
 Studio grafico-analitico delle funzioni reali a variabile reale Sequenza dei passi Classificazione In pratica Classifica il tipo di funzione: Funzione razionale: intera / fratta Funzione irrazionale: intera
Studio grafico-analitico delle funzioni reali a variabile reale Sequenza dei passi Classificazione In pratica Classifica il tipo di funzione: Funzione razionale: intera / fratta Funzione irrazionale: intera
